
����Ŀ��ij���ٹ�·ȫ������2n(n��4��![]() )��������.Ϊ��ǿ��ʻ��Ա�İ�ȫ��ʶ���ֹ滮��ÿ������������ڴ�������Ŀ����������A����������B.
)��������.Ϊ��ǿ��ʻ��Ա�İ�ȫ��ʶ���ֹ滮��ÿ������������ڴ�������Ŀ����������A����������B.
��1����ÿ����������ڴ�������������A�ĸ���Ϊ![]() ����ڴ�������������B�ķ�������X������X����ѧ������
����ڴ�������������B�ķ�������X������X����ѧ������
��2����̽��ȫ������������������ñ�����ʹ�ó�;˾�����߸ø���ȫ���У����ѡȡ3����������Ϣ��������ͬ��������ĸ�����С�����������Сֵ.
���𰸡���1��![]() ��2��������������1��1����ʱ����������ĸ�����С������СֵΪ
��2��������������1��1����ʱ����������ĸ�����С������СֵΪ![]()
��������
��1���������ÿ����������ڴ�������������B�ĸ���Ϊ![]() ����X~B(2n��
����X~B(2n��![]() )���ɴ˿�����𰸣�
)���ɴ˿�����𰸣�
��2���ɹŵ���͵ĸ��ʼ��㹫ʽ�ɵã�����3��������������ͬ������������¼���ΪM��������ͬ��������ĸ���P��![]() �� ��ø��ٹ�·ȫ��2n���������У���ڴ�������Ŀ����������A����m(m
�� ��ø��ٹ�·ȫ��2n���������У���ڴ�������Ŀ����������A����m(m![]() ��m��2n)�����������ۣ����������������������������������֮��ķ����ж��䵥���ԣ��������������ʿ����
��m��2n)�����������ۣ����������������������������������֮��ķ����ж��䵥���ԣ��������������ʿ����![]() ����Сֵ���Ӷ�����𰸣�
����Сֵ���Ӷ�����𰸣�
�⣺��1����ÿ����������ڴ�������������A�ĸ���Ϊ![]() ��
��
��ÿ����������ڴ�������������B�ĸ���Ϊ![]() ��
��
��X~B(2n��![]() )����
)����![]() ��
��
��2����;˾�����߸ø���ȫ���У������ѡȡ3��������������![]() ��ѡȡ������
��ѡȡ������
��;˾�����߸ø���ȫ���У������ѡȡ3����������
����3��������������ͬ������������¼���ΪM��
�������P��![]() ��
��
��ø��ٹ�·ȫ��2n���������У���ڴ�������Ŀ����������A����m(m![]() ��m��2n)����
��m��2n)����
�ٵ�![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]()
![]()
![]() ��
��
�൱![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
�൱![]() ʱ��
ʱ��![]() ����
����![]() ��
��
�ڵ�![]() ��
��![]() ʱ��
ʱ��![]() ����Ȼ
����Ȼ![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]()
![]()
![]() ��
��
��![]() ��
��
��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ʱ��
ʱ��![]() ����
����![]() ����
����![]() ��
��
��ͬ�ڣ�![]() ��
��
���ϣ���![]() ʱ��
ʱ��![]() ��
��![]() ��
��
��������������1��1����ʱ����������ĸ�����С������СֵΪ![]() ��
��


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�������㷨ͳ�ڡ������������⣺��Զ��ΡΡ���߲㣬����㱶�������������ٰ�ʮһ�����ʼ�ͷ��յ�ƣ�����˼�ǣ�һ��7����������381յ�ƣ������������е���һ���������һ�������2���������Ķ��㹲�еƣ� ��
A. 1յ B. 3յ C. 5յ D. 9յ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �Ľ���Ϊ4���ҹ���
�Ľ���Ϊ4���ҹ���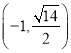 ��
��
��1������ԲE�ķ��̣�
��2����![]() ��
��![]() ��
��![]() ����B����б��Ϊ
����B����б��Ϊ![]() ��ֱ��l����ԲE����һ��M����x���ڵ�Q��ֱ��AM��ֱ��
��ֱ��l����ԲE����һ��M����x���ڵ�Q��ֱ��AM��ֱ��![]() �ཻ�ڵ�P��֤����
�ཻ�ڵ�P��֤����![]() ��OΪ����ԭ�㣩��
��OΪ����ԭ�㣩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ�����ϵ![]() �У�����
�У�����![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��ֱ��
��ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ���㣬
���㣬![]() �е�Ϊ
�е�Ϊ![]() ��
��![]() �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽�![]() ��
��![]() ��
��![]() .��
.��![]() Ϊ����ԭ�㣬����Ϊ
Ϊ����ԭ�㣬����Ϊ![]() ��������Ὠ��ֱ������ϵ
��������Ὠ��ֱ������ϵ![]() .
.
��1����![]() ��ֱ�����귽�����
��ֱ�����귽�����![]() ��ֱ�����ꣻ
��ֱ�����ꣻ
��2����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����һ��뾶ΪR������AOB��������OΪ��������Բ��Բ�ģ�AOB��![]() ��OA��OB��
��OA��OB��![]() Ϊ��ԭ�е�·.Ϊ����������ͺͽ�������Ҫ��������������
Ϊ��ԭ�е�·.Ϊ����������ͺͽ�������Ҫ��������������![]() ��ѡȡһ��M���½���·OM����OAƽ�еĵ�·MN����N���߶�OB�ϣ�����AOM��
��ѡȡһ��M���½���·OM����OAƽ�еĵ�·MN����N���߶�OB�ϣ�����AOM��![]() .
.

��1�������ƣ�����ʹ����ӵ�O�����ص�·OM��MN��������N��������·�������˵�����ɣ�
��2�������ƣ�����ʹ����ӵ�A�����ص�·![]() ��MN��������N��������·�������˵������.
��MN��������N��������·�������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����ij��Ʒ��������������ͳ�ƣ��˿Ͳ��õĸ�������![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 1 | 2 | 3 | 4 | 5 |
P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
�̳�����һ������Ʒ������1�ڸ��������Ϊ200Ԫ����2�ڻ�3�ڸ��������Ϊ250Ԫ����4�ڻ�5�ڸ��������Ϊ300Ԫ��X��ʾ����һ������Ʒ������.
��1�����¼�A�����������Ʒ��3λ�˿��У�������1λ����1�ڸ������ĸ���![]() ��
��
��2����X�ķֲ��м�����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() �ϵ��溯��������
�ϵ��溯��������![]() ������ �й��ں���
������ �й��ں���![]() �������У�������ȷ���ǣ� ��
�������У�������ȷ���ǣ� ��
�ٽ�����![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ���Եõ�����
����λ���Եõ�����![]() ��ͼ��
��ͼ��
�ں���![]() ͼ���һ���Գ��᷽��Ϊ
ͼ���һ���Գ��᷽��Ϊ![]() ��
��
�۵�![]() ʱ������
ʱ������![]() ����СֵΪ
����СֵΪ![]() ��
��
�ܺ���![]() ��
��![]() �ϵ�������.
�ϵ�������.
A.�٢�B.�ۢ�C.�ڢ�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)=aex��x��
��1����f(x)�ĵ������䣬
��2��������x����ʽaex��x+b������![]() ������b���������
������b���������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����о���Ϊ�з�һ�������磬��200ֻС�������Ͻ��п��жԱ�ʵ�飬�õ�����ͳ�����ݣ�
δ��Ⱦ���� | ��Ⱦ���� | �ܼ� | |
δע������ | 30 |
|
|
ע������ | 70 |
|
|
�ܼ� | 100 | 100 | 200 |
�ִ�δע�������С��������ȡ1ֻ��ȡ������Ⱦ��������С����ĸ���Ϊ![]() .
.
�������ܷ���![]() �İ�����Ϊע�����������Ч��
�İ�����Ϊע�����������Ч��
��������δע��������δ��Ⱦ������ע�������Ҹ�Ⱦ������С�����У��ֱ��ȡ3ֻ���в���������Ȼ�����6ֻС�����������ȡ2ֻ��ע������������к�ʵ����鵽��2ֻ����ע�������Ҹ�Ⱦ������С����ĸ���.
����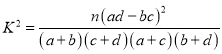 ��
��![]() ��
��
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com