
设二次函数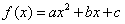 (
(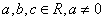 )满足条件:
)满足条件:
(1)当 时,
时,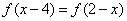 ,且
,且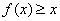 ;
;
(2)当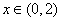 时,
时,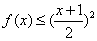 ;
;
(3)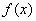 在R上的最小值为0,求最大的
在R上的最小值为0,求最大的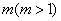 ,使得存在
,使得存在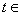 R,只要
R,只要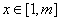 ,就有
,就有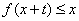 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
如图,已知O(0,0),E(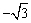 ,0),F(
,0),F(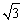 ,0),圆F:
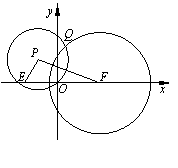
,0),圆F: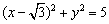 .动点P满足PE+PF=4.以P为圆心,OP为半径的圆P与圆F的一个公共点为Q.
.动点P满足PE+PF=4.以P为圆心,OP为半径的圆P与圆F的一个公共点为Q.
(1)求点P的轨迹方程;
(2)证明:点Q到直线PF的距离为定值,并求此值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某服装加工厂某月生产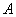 、
、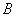 、
、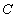 三种产品共4000件,为了保证产品质量,进行抽样检验,根据分层抽样的结果,企业统计员制作了如下的统计表格:
三种产品共4000件,为了保证产品质量,进行抽样检验,根据分层抽样的结果,企业统计员制作了如下的统计表格:
| 产品类别 |
|
|
|
| 产品数量(件) |
| ||
| 样本容量(件) | 230 |
由 于不小心,表格中
于不小心,表格中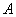 、
、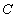 产品的有关数据已被污染看不清楚,统计员记得
产品的有关数据已被污染看不清楚,统计员记得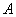 产品
产品 的样本容量
的样本容量 比
比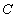 产品的样本容量多
产品的样本容量多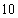 ,根据以上信息,可得
,根据以上信息,可得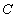 的产品数量是________.
的产品数量是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com