
|
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”
某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
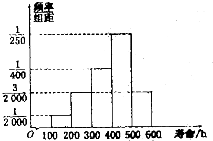 对某种电子元件的使用寿命进行跟踪调查,所得样本的频率分布直方图如图所示,由图可知,这一批电子元件中使用寿命在100~300h的电子元件的数量与使用寿命在300~600h的电子元件的数量的比是
对某种电子元件的使用寿命进行跟踪调查,所得样本的频率分布直方图如图所示,由图可知,这一批电子元件中使用寿命在100~300h的电子元件的数量与使用寿命在300~600h的电子元件的数量的比是查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com