
分析 (1)联立直线方程与椭圆方程,由判别式大于0求得实数m的取值范围;
(2)由(1)中的方程结合根与系数的关系可得直线l被椭圆所截线段中点的坐标,代入直线3x+2y=0成立,说明直线被椭圆截得的线段的中点都在直线3x+2y=0上.
解答 (1)解:将$y=\frac{3}{2}x+m$代入$\frac{x^2}{4}+\frac{y^2}{9}=1$,整理得:9x2+6mx+2m2-18=0,
由△=36m2-36(2m2-18)=-36m2+36×18>0,
解得$-3\sqrt{2}<m<3\sqrt{2}$,
∴实数m的取值范围是($-3\sqrt{2},3\sqrt{2}$);
(2)证明:设直线l与椭圆C相交于A(x1,y1),B(x2,y2),由(1)知${x_1}+{x_2}=-\frac{2m}{3}$,
∴${y_1}+{y_2}=\frac{3}{2}({x_1}+{x_2})+2m=m$,
故线段AB的中点$M(-\frac{m}{3},\frac{m}{2})$,
代入直线3x+2y=0,可得3×$(-\frac{m}{3})+2×\frac{m}{2}=0$.
∴直线被椭圆截得的线段的中点都在直线3x+2y=0上.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,是中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{13}{12}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
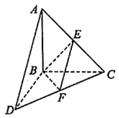 如图,三棱锥A-BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4$\sqrt{2}$,CD=4$\sqrt{3}$,∠ACB=45°,E,F分别为MN的中点.
如图,三棱锥A-BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4$\sqrt{2}$,CD=4$\sqrt{3}$,∠ACB=45°,E,F分别为MN的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-2,1 ) | B. | (-3,2,-1) | C. | (-3,-2,-1) | D. | (-3,2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com