
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某3D打印机,其打出的产品质量按照百分制衡量,若得分不低于85分则为合格品,低于85分则为不合格品,商家用该打印机随机打印了15件产品,得分情况如图;
某3D打印机,其打出的产品质量按照百分制衡量,若得分不低于85分则为合格品,低于85分则为不合格品,商家用该打印机随机打印了15件产品,得分情况如图;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:解答题
已知函数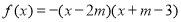 (其中
(其中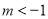 ),
),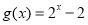 .
.
(1)若命题“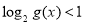 ”是真命题,求
”是真命题,求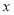 的取值范围;
的取值范围;
(2)设命题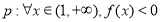 或
或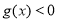 ;命题
;命题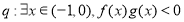 ,若
,若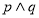 是真命题,求
是真命题,求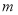 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:选择题
已知关于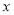 的方程
的方程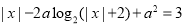 有唯一实数解,则实数
有唯一实数解,则实数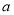 的值为( )
的值为( )
A.-1 B.1
C.-1或3 D.1或-3
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:解答题
某公司2016年前三个月的利润(单位:百万元)如下:
(1)求利润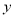 关于月份
关于月份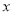 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式:
 ,
,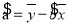 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com