练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．如图，位于A处前方有两个观察站B，D，且△ABD为边长等于3km的正三角形，当发现目标出现于C处时，测得∠BDC=45°，∠CBD=75°，则AC=（　　）
    A．15-6$\sqrt{3}$kmB．15+6$\sqrt{3}$kmC．$\sqrt{15+6\sqrt{3}}$kmD．$\sqrt{15-6\sqrt{3}}$km

    分析 先利用正弦定理，求出DC，再用余弦定理，求出AC．

    解答 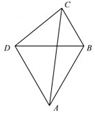解：由题意，∠BCD=60°，∴$\frac{3}{sin60°}$=$\frac{DC}{sin75°}$，
    ∴DC=$\frac{1}{2}$（3$\sqrt{2}$+$\sqrt{6}$），
    ∵∠CDA=105°，
    ∴AC=$\sqrt{（\frac{3\sqrt{2}+\sqrt{6}}{2}）^{2}+9-2•\frac{3\sqrt{2}+\sqrt{6}}{2}•3•（-\frac{\sqrt{6}+\sqrt{2}}{4}）}$=$\sqrt{15+6\sqrt{3}}$，
    故选C．

    点评 本题考查正弦、余弦定理的运用，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．有一组数据：
    x81213a18
    y108674
    已知y对x呈线性相关关系为：$\hat y=13.5-0.5x$，则a的值为14．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知点M（a，b）在直线3x+4y-15=0上，则$\sqrt{（a-1）^{2}+（b+2）^{2}}$的最小值是4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=ax3+x2（a∈R）在x=-$\frac{4}{3}$处取得极值．
    （1）确定a的值和f（x）的极值；
    （2）若g（x）=f（x）ex，讨论g（x）的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．柜子里有3双不同的鞋，随机地取2只，下列叙述错误的是（　　）
    A．取出的鞋不成对的概率是$\frac{4}{5}$
    B．取出的鞋都是左脚的概率是$\frac{1}{5}$
    C．取出的鞋都是同一只脚的概率是$\frac{2}{5}$
    D．取出的鞋一只是左脚的，一只是右脚的，但它们不成对的概率是$\frac{12}{25}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知f（x）是定义域为（0，+∞）的单调函数，若对任意的x∈（0，+∞），都有$f[{f（x）+{{log}_{\frac{1}{3}}}x}]=4$，且方程|f（x）-3|=x3-6x2+9x-4+a在区间（0，3]上有两解，则实数a的取值范围是（　　）
    A．0＜a≤5B．a＜5C．0＜a＜5D．a≥5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．若多项式${x^2}+{x^{11}}={a_0}+{a_1}（x+1）+…{a_{10}}{（x+1）^{10}}+{a_{11}}{（x+1）^{11}}$，则a10=-11．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知圆C的圆心C在x轴上，且圆C与直线$x+\sqrt{3}y+n=0$相切于点$（{\frac{3}{2}，\frac{{\sqrt{3}}}{2}}）$．
    （1）求n的值及圆C的方程；
    （2）若圆M：${x^2}+{（{y-\sqrt{15}}）^2}={r^2}（{r＞0}）$与圆C相切，求直线$\sqrt{3}x-\sqrt{2}y=0$截圆M所得的弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知集合A={-2，0，2}，B={x|x2-2x-3≤0}，则A∩B=（　　）
    A．{0}B．{2}C．{0，2}D．{-2，0}

    查看答案和解析>>

    同步练习册答案