练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设直线l:2x+y-2=0与椭圆x2+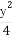=1的交点为A,B,点P是椭圆上的动点,则使得△PAB的面积为的点P的个数为　　　.

     

    4

    【解析】【思路点拨】先求出弦长|AB|,进而求出点P到直线AB的距离,再求出与l平行且与椭圆相切的直线方程,最后数形结合求解.

    由题知直线l恰好经过椭圆的两个顶点(1,0),(0,2),故|AB|=,要使

    △PAB的面积为,即··h=,所以h=.联立y=-2x+m与椭圆方程x2+=1得8x2-4mx+m2-4=0,令Δ=0得m=±2,即平移直线l到y=-2x±2时与椭圆相切,它们与直线l的距离d=都大于,所以一共有4个点符合要求.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业六十一第九章第二节练习卷（解析版） 题型：选择题

    将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为(　　)

    (A)26,16,8 (B)25,17,8

    (C)25,16,9 (D)24,17,9

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业五十四第八章第五节练习卷（解析版） 题型：解答题

    已知椭圆C: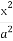+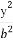=1(a>b>0).

    (1)若椭圆的长轴长为4,离心率为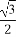,求椭圆的标准方程.

    (2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.

    (3)过原点O任意作两条互相垂直的直线与椭圆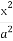+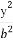=1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业五十六第八章第七节练习卷（解析版） 题型：填空题

    以抛物线x2=16y的焦点为圆心,且与抛物线的准线相切的圆的方程为_________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业五十六第八章第七节练习卷（解析版） 题型：选择题

    设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是(　　)

    (A)4 (B)6 (C)8 (D)12

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业五十八第八章第九节练习卷（解析版） 题型：选择题

    已知m,n为两个不相等的非零实数,则方程mx-y+n=0与nx2+my2=mn所表示的曲线可能是(　　)

     

     

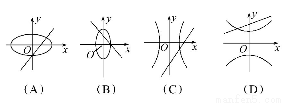
    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业五十五第八章第六节练习卷（解析版） 题型：解答题

    已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为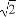,且过点P(4,-).

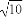    (1)求双曲线的方程.

    (2)若点M(3,m)在双曲线上,求证: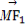·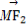=0.

    (3)求△F1MF2的面积.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷（解析版） 题型：填空题

    圆C:x2+y2+2x-2y-2=0的圆心到直线3x+4y+14=0的距离是　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷（解析版） 题型：解答题

    已知椭圆的中心为坐标原点,短轴长为2,一条准线的方程为l:x=2.

    (1)求椭圆的标准方程.

    (2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.

     

    查看答案和解析>>

    同步练习册答案