
已知椭圆C: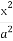 +
+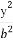 =1(a>b>0).
=1(a>b>0).
(1)若椭圆的长轴长为4,离心率为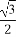 ,求椭圆的标准方程.
,求椭圆的标准方程.
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
(3)过原点O任意作两条互相垂直的直线与椭圆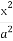 +
+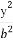 =1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
=1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
(1)  +y2=1 (2) k∈(-2,-
+y2=1 (2) k∈(-2,- )∪(
)∪( ,2) (3)
,2) (3) 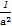 +
+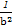 =1
=1
【解析】(1)由已知2a=4,∴a=2,
又e=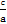 =
= ,∴c=
,∴c=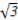 .
.
因此,b2=a2-c2=4-3=1,
∴椭圆的标准方程为 +y2=1.
+y2=1.
(2)显然直线x=0不满足题设条件,
可设直线l:y=kx+2,A(x1,y1),B(x2,y2).
由 消去y得(1+4k2)x2+16kx+12=0.
消去y得(1+4k2)x2+16kx+12=0.
∵Δ=(16k)2-4×12(1+4k2)>0,
∴k∈(-∞,- )∪(
)∪( ,+∞) ①
,+∞) ①
又x1+x2=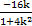 ,x1x2=
,x1x2=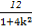 ,
,
由0°<∠AOB<90°⇒ ·
·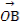 >0,
>0,
∴ ·
·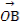 =x1x2+y1y2>0,
=x1x2+y1y2>0,
所以 ·
·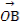 =x1x2+y1y2
=x1x2+y1y2
=x1x2+(kx1+2)(kx2+2)
=(1+k2)x1x2+2k(x1+x2)+4,
∴-2<k<2 ②
由①②得k∈(-2,- )∪(
)∪( ,2).
,2).
(3)由椭圆的对称性可知PQSR是菱形,原点O到各边的距离相等.
当P在y轴上,Q在x轴上时,直线PQ的方程为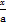 +
+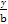 =1,由d=1得
=1,由d=1得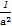 +
+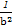 =1,
=1,
当P不在y轴上时,设直线PS的斜率为k,P(x1,kx1),则直线RQ的斜率为-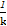 ,Q(x2,-
,Q(x2,-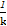 x2),
x2),
由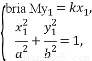 得
得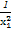 =
=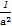 +
+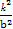 ①
①
同理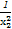 =
=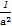 +
+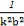 ②
②
在Rt△OPQ中,由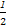 d·|PQ|=
d·|PQ|=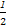 |OP|·|OQ|,
|OP|·|OQ|,
即|PQ|2=|OP|2·|OQ|2.
所以(x1-x2)2+(kx1+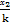 )2
)2
=[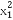 +(kx1)2]·[
+(kx1)2]·[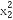 +(
+(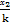 )2],
)2],
化简得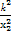 +
+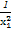 =1+k2,
=1+k2,
k2(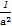 +
+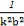 )+
)+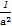 +
+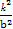 =1+k2,
=1+k2,
即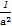 +
+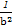 =1.
=1.
综上,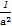 +
+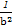 =1.
=1.
【方法技巧】平面向量在平面解析几何中的应用
平面向量作为数学解题的工具,常与平面解析几何结合综合考查,主要涉及向量的数量积、夹角、长度、距离等方面的知识,应用方向主要是平面内点的坐标与对应向量数量积的转化,通过数量积运算寻找等量关系,使问题转化,从而使问题获解.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十九第十章第六节练习卷(解析版) 题型:选择题
已知P是△ABC所在平面内一点,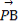 +
+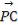 +2
+2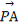 =0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )
=0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业八十选修4-5第二节练习卷(解析版) 题型:解答题
已知f(x)=|x+1|+|x-1|,不等式f(x)<4的解集为M.
(1)求M.
(2)当a,b∈M时,证明:2|a+b|<|4+ab|.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十第八章第一节练习卷(解析版) 题型:填空题
经过点(-2,2),且与两坐标轴所围成的三角形面积为1的直线l的方程为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十第八章第一节练习卷(解析版) 题型:选择题
已知△ABC三顶点坐标A(1,2),B(3,6),C(5,2),M为AB中点,N为AC中点,则直线MN的方程为( )
(A)2x+y-8=0 (B)2x-y+8=0
(C)2x+y-12=0 (D)2x-y-12=0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十四第八章第五节练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为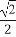 .过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为 .
.过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十六第八章第七节练习卷(解析版) 题型:解答题
如图,椭圆C: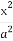 +
+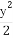 =1的焦点在x轴上,左右顶点分别为A1,A,上顶点为B,抛物线C1,C2分别以A,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线y=
=1的焦点在x轴上,左右顶点分别为A1,A,上顶点为B,抛物线C1,C2分别以A,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线y=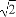 x上一点P.
x上一点P.
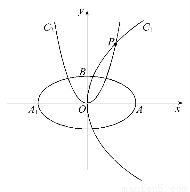
(1)求椭圆C及抛物线C1,C2的方程.
(2)若动直线l与直线OP垂直,且与椭圆C交于不同两点M,N,已知点Q(-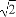 ,0),求
,0),求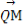 ·
·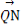 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十八第八章第九节练习卷(解析版) 题型:填空题
设直线l:2x+y-2=0与椭圆x2+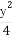 =1的交点为A,B,点P是椭圆上的动点,则使得△PAB的面积为
=1的交点为A,B,点P是椭圆上的动点,则使得△PAB的面积为 的点P的个数为 .
的点P的个数为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十九第八章第十节练习卷(解析版) 题型:解答题
给定椭圆C: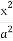 +
+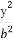 =1(a>b>0),称圆心在原点O,半径为
=1(a>b>0),称圆心在原点O,半径为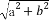 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(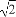 ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为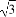 .
.
(1)求椭圆C的方程和其“准圆”的方程.
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1,l2使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于点M,N.
①当P为“准圆”与y轴正半轴的交点时,求l1,l2的方程;
②求证:|MN|为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com