
 棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,求图中三角形(正四面体的截面)的面积.
棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,求图中三角形(正四面体的截面)的面积. 分析 将截面图转化为立体图,求三角形面积就是求正四面体中的△ABD的面积,求得AD,AC,由勾股定理可得CD,再由三角形的面积公式,计算即可得到所求.
解答 解:如图球的截面图就是正四面体中的△ABD,
已知正四面体棱长为2,
所以AD=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$,AC=1,
在直角三角形ACD中,
CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=$\sqrt{3-1}$=$\sqrt{2}$,
可得截面面积是:S△ABD=$\frac{1}{2}$×2×$\sqrt{2}$=$\sqrt{2}$.
点评 本题考查球内接多面体以及棱锥的特征,考查空间想象能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(3) | C. | f(-2)<f(1)<f(3) | D. | f(3)<f(1)<f(-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,$\frac{CD}{DA}$=$\frac{AE}{EB}$=$\frac{1}{2}$,记$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,则$\overrightarrow{ED}$=$\frac{\overrightarrow{a}-\overrightarrow{b}}{3}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示).
如图,在△ABC中,$\frac{CD}{DA}$=$\frac{AE}{EB}$=$\frac{1}{2}$,记$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,则$\overrightarrow{ED}$=$\frac{\overrightarrow{a}-\overrightarrow{b}}{3}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
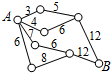 如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 19 | B. | 20 | C. | 24 | D. | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com