
分析 (1)设焦距为2c,结合e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,从而求椭圆的方程;
(2)联立方程化简可得(1+3k2)x2+12kx+9=0,再设C(x1,y1),D(x2,y2);从而可得x1+x2=-$\frac{12k}{3{k}^{2}+1}$,x1x2=$\frac{9}{3{k}^{2}+1}$;从而由平面向量化简可得(k2+1)$\frac{9}{3{k}^{2}+1}$-(2k+1)$\frac{12k}{3{k}^{2}+1}$+5=0,从而解得.
解答 解:(1)设焦距为2c,
∵e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,a2=b2+c2,
∴$\frac{b}{a}$=$\frac{\sqrt{3}}{3}$;
∵|AB|=$\frac{2\sqrt{3}}{3}$,
∴2$\frac{{b}^{2}}{a}$=$\frac{2\sqrt{3}}{3}$,
解得,b=1,a=$\sqrt{3}$;
故椭圆的方程为$\frac{{x}^{2}}{3}$+y2=1;
(2)将y=kx+2代入椭圆方程,
化简可得(1+3k2)x2+12kx+9=0,
由直线与椭圆有两个交点知,
△=(12k)2-36(1+3k2)>0,
解得,k2>1;
设C(x1,y1),D(x2,y2);
则x1+x2=-$\frac{12k}{3{k}^{2}+1}$,x1x2=$\frac{9}{3{k}^{2}+1}$;
若以线段CD为直径的圆过点E(-1,0),
则$\overrightarrow{EC}$•$\overrightarrow{ED}$=0,
即(x1+1)(x2+1)+y1y2=0,
而y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4,
则(x1+1)(x2+1)+y1y2
=(k2+1)x1x2+(2k+1)(x1+x2)+5
=(k2+1)$\frac{9}{3{k}^{2}+1}$-(2k+1)$\frac{12k}{3{k}^{2}+1}$+5=0,
解得,k=$\frac{7}{6}$,满足k2>1;
故k=$\frac{7}{6}$.
点评 本题考查了圆锥曲线与直线的位置关系的应用及平面向量的应用,同时考查了学生的化简运算能力.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{15}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
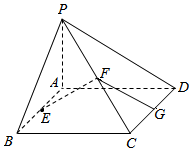 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F、G分别是AB、PC、CD的中点,|PA|=|AB|=|AD|=1,
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F、G分别是AB、PC、CD的中点,|PA|=|AB|=|AD|=1,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com