
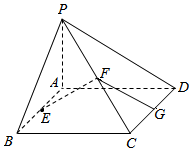
 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F、G分别是AB、PC、CD的中点,|PA|=|AB|=|AD|=1,
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F、G分别是AB、PC、CD的中点,|PA|=|AB|=|AD|=1,分析 (1)g根据线面平行的判定定理即可证明EF∥平面PAD;
(2)根据线面垂直的性质定理即可证明F⊥CD,EF⊥PD,且|EF|=$\frac{1}{2}$|PD|;
(3)根据异面直线所成的角即可求直线PD与AC所成的角;
(4)根据直线和平面所成角的定义即可求直线AP与平面PCD所成的角;
(5)根据二面角的定义即可求平面PAB与平面PCD所成的角.
解答 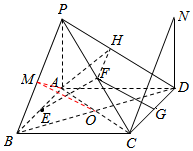 解:(1)证明:取PD中点H,连FH,AH
解:(1)证明:取PD中点H,连FH,AH
则FH平行且等于$\frac{1}{2}$CD,
又CD平行且等于AB,E为AB中点,
∴FH平行且等于AE
∴AEFH为平行四边形,
从而EF∥AH,
又EF?平面PAD,AH?平面PAD,
∴EF∥平面PAD
(2)∵CD⊥AD,CD⊥PA,PA∩AD=A
PA在平面PAD内,AD在平面PAD内
∴CD⊥面PAD
又∵AH?平面PAD,
∴CD⊥AH
∵EF∥AH
∴CD⊥EF;
∵PA|=|AB|=|AD|=1,H是中点,
∴AH⊥PD,且|AH|=$\frac{1}{2}$|PD|;
∵EF∥AH且EF=AH,
∴EF⊥PD,且|EF|=$\frac{1}{2}$|PD|;
(3)取PB的中点M,连接AM,OM,
则OM∥PD,
则OM与OC所成的角就是PD与AC所成的角,
则OM=$\frac{1}{2}$|PD|=$\frac{\sqrt{2}}{2}$,
PB=$\sqrt{2}$,AM=$\frac{1}{2}$PB=$\frac{\sqrt{2}}{2}$,OA=$\frac{1}{2}AC$=$\frac{\sqrt{2}}{2}$,
则OA=AM=OM,则△OAM为正三角形,
则∠AOM=60°,即直线PD与AC所成的角为60°.
(4)由(2)知AH⊥平面PAD,
则PH是PA在平面PAD上的射影,
则∠PAH为直线AP与平面PCD所成的角,
∵PA=AD,∴∠PAH=45°,
即直线AP与平面PCD所成的角为45°.
(5)过D作DN⊥平面ABCD,
则∠PDN是平面PCD与平面PCD所成的角,
同时也是平面PAB与平面PCD所成的角,
∵∠PDN=∠PAH=45°,
∴平面PAB与平面PCD所成的角是45°.
点评 本题主要考查空间直线,平面平行或垂直的位置关系的判断,以及空间角的求解,根据相应的定理和定义是解决本题的关键.综合性较强,运算量较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
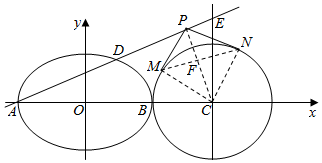 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A、B分别其左右顶点,直线AE交其右准线CE于点E,交椭圆于点D($\frac{1}{e}$,3),其中e为椭圆的离心率,B为线段OC的中点.圆C是以C点为圆心,CB长为半径的圆,P为直线AE上任意一点,过P向圆C作切线,切点分别为M、N.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A、B分别其左右顶点,直线AE交其右准线CE于点E,交椭圆于点D($\frac{1}{e}$,3),其中e为椭圆的离心率,B为线段OC的中点.圆C是以C点为圆心,CB长为半径的圆,P为直线AE上任意一点,过P向圆C作切线,切点分别为M、N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
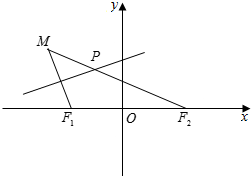 如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.
如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
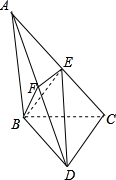 如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.
如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知O为坐标原点,F为椭圆C:x2+$\frac{y^2}{2}$=1在y轴正半轴上的焦点,过F且斜率为-$\sqrt{2}$的直线l与C交与A、B两点,四边形OAPB为平行四边形.
已知O为坐标原点,F为椭圆C:x2+$\frac{y^2}{2}$=1在y轴正半轴上的焦点,过F且斜率为-$\sqrt{2}$的直线l与C交与A、B两点,四边形OAPB为平行四边形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
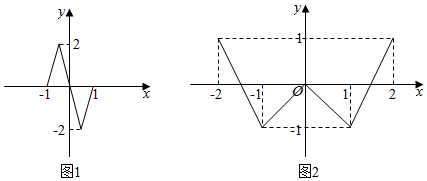
| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com