
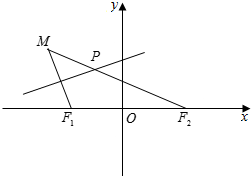
 如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.
如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.分析 (Ⅰ)连接PF1,运用垂直平分线定理和椭圆的定义,可得P的轨迹为椭圆,方程为$\frac{x^2}{2}+{y^2}=1$;
(Ⅱ)联立直线方程和椭圆方程,消去y,得(1+2k2)x2+4kmx+2m2-2=0,运用韦达定理和直线的斜率公式,化简整理,再由直线恒过定点的方法,即可得到所求定点.
解答 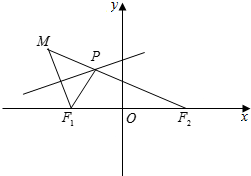 解:(Ⅰ)连接PF1,由$|M{F_2}|=2\sqrt{2}$,
解:(Ⅰ)连接PF1,由$|M{F_2}|=2\sqrt{2}$,
∴$|PM|+|P{F_2}|=2\sqrt{2}$,
又∵|PM|=|PF1|,∴$|P{F_1}|+|P{F_2}|=2\sqrt{2}>|{F_1}{F_2}|=2$,
由椭圆的定义可知2a=2$\sqrt{2}$,c=1,b=1.
即有动点P的轨迹G的方程为$\frac{x^2}{2}+{y^2}=1$;
(Ⅱ)证明:依题意$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,消去y,得
(1+2k2)x2+4kmx+2m2-2=0,
设M(x1,y1),N(x2,y2),
则x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$,
又${k}_{{F}_{1}M}$=$\frac{k{x}_{1}+m}{{x}_{1}-1}$,${k}_{{F}_{1}N}$=$\frac{k{x}_{2}+m}{{x}_{2}-1}$
依题意得,${k}_{{F}_{1}M}$+${k}_{{F}_{1}N}$=0,
即$\frac{k{x}_{1}+m}{{x}_{1}-1}$+$\frac{k{x}_{2}+m}{{x}_{2}-1}$=0,
化简得:2kx1x2+(m-k)(x1+x2)-2m=0,
∴2k•$\frac{2{m}^{2}-2}{1+2{k}^{2}}$+(m-k)(-$\frac{4km}{1+2{k}^{2}}$)-2m=0,
整理得,m=-2k,
∴直线l的方程为y=k(x-2),
因此直线l经过定点,该定点坐标为(2,0).
点评 本题考查轨迹方程的求法,注意运用垂直平分线定理和椭圆的定义,考查直线恒过定点的求法,注意运用直线和椭圆方程联立,运用韦达定理和直线的斜率公式,考查化简整理的运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
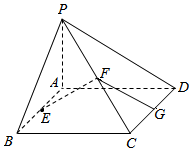 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F、G分别是AB、PC、CD的中点,|PA|=|AB|=|AD|=1,
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F、G分别是AB、PC、CD的中点,|PA|=|AB|=|AD|=1,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$) | B. | (0,$\frac{1}{2}$] | C. | ($\frac{1}{3}$,$\frac{1}{2}$] | D. | [$\frac{1}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
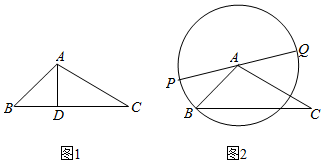 在△ABC中.
在△ABC中.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
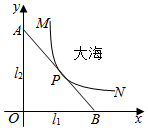 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,点P到l2的距离为2千米.以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,点P到l2的距离为2千米.以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com