
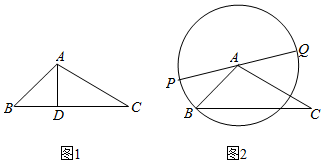
 �ڡ�ABC�У�
�ڡ�ABC�У����� ��1������ֱ������ϵ�����õ�������ʾ������Ȼ�������������ֵ��
��2������������ת��Ϊ��֪�����Ĺ�ϵ��ͨ���������������Ƴ��������ı���ʽ��Ȼ�������ֵ��
��� 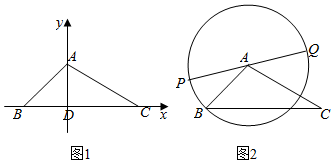 �⣺��1����BC��DA�ֱ�Ϊx��y����ͼ��
�⣺��1����BC��DA�ֱ�Ϊx��y����ͼ��
|$\overrightarrow{AC}$|=2��AD��BC��D����BAD=45�㣬��DAC=60�㣬
�ɵ�A��0��1����B��-1��0����C��$\sqrt{3}$��0����
D��0��0����
$\overrightarrow{BD}$•$\overrightarrow{AC}$=��1��0����-1��$\sqrt{3}$��=-1��
$\overrightarrow{BA}$•$\overrightarrow{AC}$=��1��1����-1��$\sqrt{3}$��=$\sqrt{3}-1$��
��2����$\overrightarrow{AQ}$��x��������ɽǦȣ�������$\overrightarrow{PQ}$��$\overrightarrow{BC}$�ļн�Ϊ���ȣ�
$\overrightarrow{BP}•\overline{CQ}$=��$\overrightarrow{AP}$-$\overrightarrow{AB}$��•��$\overrightarrow{AQ}$-$\overrightarrow{AC}$��=��$\overrightarrow{AP}$-$\overrightarrow{AB}$��•��-$\overrightarrow{AP}$-$\overrightarrow{AC}$��
=-$\overrightarrow{AP}$2+��$\overrightarrow{AB}$-$\overrightarrow{AC}$��$\overrightarrow{AP}$+$\overrightarrow{AC}$•$\overrightarrow{AB}$
=-${\overrightarrow{AP}}^{2}$+$\overrightarrow{CB}$•$\overrightarrow{AP}$+$\overrightarrow{AC}•\overrightarrow{AB}$--------��6�֣�
��${\overrightarrow{AP}}^{2}$=2��$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos��BAC
=2$\sqrt{2}$cos105��
=1-$\sqrt{3}$----------��8�֣�
��$\overrightarrow{BP}$•$\overrightarrow{CQ}$=-2+$\overrightarrow{CB}$•$\overrightarrow{AP}$+1-$\sqrt{3}$=-1-$\sqrt{3}$+|$\overrightarrow{CB}$|•|$\overrightarrow{AP}$|cos��
=-1-$\sqrt{3}$+��1+$\sqrt{3}$����$\sqrt{2}$cos��=-1-$\sqrt{3}$+��1+$\sqrt{3}$��cos��---��10�֣�
��$\overrightarrow{CB}$��$\overrightarrow{AP}$������ͬʱ��$\overrightarrow{BP}$•$\overrightarrow{CQ}$ȡ�����ֵ0����ʱ$\overrightarrow{PQ}$��$\overrightarrow{BC}$�ķ�����ͬ��------��11�֣�
��$\overrightarrow{CB}$��$\overrightarrow{AP}$�����෴ʱ��$\overrightarrow{BP}$•$\overrightarrow{CQ}$ȡ����Сֵ-2-2$\sqrt{3}$����ʱ$\overrightarrow{PQ}$��$\overrightarrow{BC}$�ķ����෴------��12�֣�
���� ���⿼�������ڼ����е�Ӧ�ã����������������Լ���������Ӧ�ã�����ת��˼���Լ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
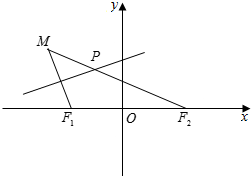 ��ͼ��ʾ����F1��-1��0����F2��1��0��������M����F2�ľ�����$2\sqrt{2}$���߶�MF1���д��߽�MF2�ڵ�P��
��ͼ��ʾ����F1��-1��0����F2��1��0��������M����F2�ľ�����$2\sqrt{2}$���߶�MF1���д��߽�MF2�ڵ�P���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪OΪ����ԭ�㣬FΪ��ԲC��x2+$\frac{y^2}{2}$=1��y���������ϵĽ��㣬��F��б��Ϊ-$\sqrt{2}$��ֱ��l��C����A��B���㣬�ı���OAPBΪƽ���ı��Σ�
��֪OΪ����ԭ�㣬FΪ��ԲC��x2+$\frac{y^2}{2}$=1��y���������ϵĽ��㣬��F��б��Ϊ-$\sqrt{2}$��ֱ��l��C����A��B���㣬�ı���OAPBΪƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ҫ��������� | B�� | ��ֲ���Ҫ���� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{8}$ | B�� | $\frac{3}{8}$ | C�� | $\frac{5}{8}$ | D�� | $\frac{7}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �������� | C�� | �ڶ����� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
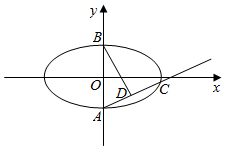 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲW��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{6}}{3}$������Բ�ҽ����Ҵ�ֱ��x���ֱ�߽���Բ���õ��ҵ��ҳ�Ϊ$\frac{2\sqrt{3}}{3}$������A��ֱ������ԲW������һ��C��
��ͼ����ƽ��ֱ������ϵxOy�У���ԲW��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{6}}{3}$������Բ�ҽ����Ҵ�ֱ��x���ֱ�߽���Բ���õ��ҵ��ҳ�Ϊ$\frac{2\sqrt{3}}{3}$������A��ֱ������ԲW������һ��C���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com