
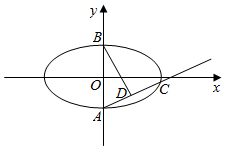
 如图,在平面直角坐标系xOy中,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{6}}{3}$,过椭圆右焦点且垂直于x轴的直线交椭圆所得的弦的弦长为$\frac{2\sqrt{3}}{3}$,过点A的直线与椭圆W交于另一点C,
如图,在平面直角坐标系xOy中,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{6}}{3}$,过椭圆右焦点且垂直于x轴的直线交椭圆所得的弦的弦长为$\frac{2\sqrt{3}}{3}$,过点A的直线与椭圆W交于另一点C,分析 (Ⅰ)运用离心率公式,将x=$\sqrt{6}$k代入椭圆方程,求得弦长,解方程可得k,进而得到a,b,可得椭圆方程;
(Ⅱ)求得AC的方程,代入椭圆方程,求得C的坐标,由两点的距离公式,计算即可得到所求值;
(Ⅲ)依题意,设直线AC的方程为y=kx-1,k≠0.代入椭圆方程,求得C,D的坐标,再由以AB为直径的圆恰过点D,|OD|=1,运用两点的距离公式计算即可得到所求斜率.
解答 解:(Ⅰ)由e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,设a=3k(k>0),则c=$\sqrt{6}$k,b=$\sqrt{3}$k,
所以椭圆W的方程为$\frac{{x}^{2}}{9{k}^{2}}$+$\frac{{y}^{2}}{3{k}^{2}}$=1,
把x=$\sqrt{6}$k代入椭圆方程,
解得y=±k,于是2k=$\frac{2\sqrt{3}}{3}$,即k=$\frac{\sqrt{3}}{3}$,
所以椭圆W的方程为$\frac{{x}^{2}}{3}$+y2=1;
(Ⅱ)由已知A(0,-1),
直线AC的方程为y=$\frac{1}{3}$x-1.
由$\left\{\begin{array}{l}{y=\frac{1}{3}x-1}\\{{x}^{2}+3{y}^{2}=3}\end{array}\right.$得2x2-3x=0,解得x=$\frac{3}{2}$或x=0(舍),
所以点C的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),
所以|AC|=$\sqrt{(\frac{3}{2})^{2}+(-\frac{1}{2}+1)^{2}}$=$\frac{\sqrt{10}}{2}$.
(Ⅲ)依题意,设直线AC的方程为y=kx-1,k≠0.
由$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+3{y}^{2}=3}\end{array}\right.$得(1+3k2)x2-6kx=0,
解得x=$\frac{6k}{1+3{k}^{2}}$或x=0(舍),所以点C的横坐标为$\frac{6k}{1+3{k}^{2}}$,
设点D的坐标为(x0,y0),则x0=$\frac{3k}{3{k}^{2}+1}$,
y0=kx0-1=$\frac{-1}{3{k}^{2}+1}$,
因为以AB为直径的圆恰过点D,所以|OD|=1,
即($\frac{3k}{1+3{k}^{2}}$)2+($\frac{-1}{1+3{k}^{2}}$)2=1.
整理得k2=$\frac{1}{3}$,
所以k=±$\frac{\sqrt{3}}{3}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和弦长的求法,考查直线方程的运用,注意联立直线方程和椭圆方程,考查运算化简能力,属于中档题.


科目:高中数学 来源: 题型:解答题
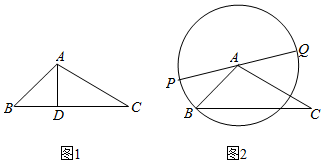 在△ABC中.
在△ABC中.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
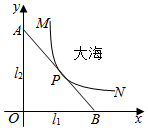 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,点P到l2的距离为2千米.以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,点P到l2的距离为2千米.以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
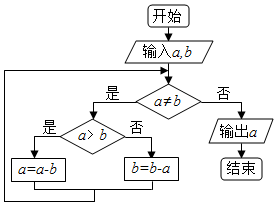 上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )
上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )| A. | 0 | B. | 1 | C. | 3 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com