
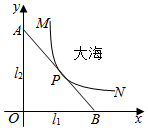
 ij�غ����еĺ������������ֱ��ֱ����·l1��l2�������߽�MPN���Ƶؿ���һ�����߶Σ�Ϊ����������Դ������һ������������·��ֱ���۹���AB����ֱ��AB������MPN���ҽ���һ��������P����ֱ�����������У�����ͼ��ʾ�������߶�MPN�Ǻ���$y=\frac{a}{x}$ͼ���һ�Σ���M��l1��l2�ľ���ֱ�Ϊ8ǧ��1ǧ�ף���N��l2�ľ���Ϊ10ǧ�ף���P��l2�ľ���Ϊ2ǧ�ף���l1��l2�ֱ�Ϊx��y�Ὠ����ͼ��ʾ��ƽ��ֱ������ϵxOy��
ij�غ����еĺ������������ֱ��ֱ����·l1��l2�������߽�MPN���Ƶؿ���һ�����߶Σ�Ϊ����������Դ������һ������������·��ֱ���۹���AB����ֱ��AB������MPN���ҽ���һ��������P����ֱ�����������У�����ͼ��ʾ�������߶�MPN�Ǻ���$y=\frac{a}{x}$ͼ���һ�Σ���M��l1��l2�ľ���ֱ�Ϊ8ǧ��1ǧ�ף���N��l2�ľ���Ϊ10ǧ�ף���P��l2�ľ���Ϊ2ǧ�ף���l1��l2�ֱ�Ϊx��y�Ὠ����ͼ��ʾ��ƽ��ֱ������ϵxOy������ ��1���������M��1��8������a=8�������߶�MPN�ĺ�����ϵʽΪ$y=\frac{8}{x}$���ɵ��䶨����
��2������ֱ�ߺ��������У������б�ʽ��=0������⼴�ɣ�
��� �⣺��1���������M��1��8������a=8�������߶�MPN�ĺ�����ϵʽΪ$y=\frac{8}{x}$��
�ֵ�$N��10��\frac{4}{5}��$�����Զ�����Ϊ[1��10]��
��2���ɣ�1��֪P��2��4������ֱ�߷���Ϊy-4=k��x-2����
��������$y=\frac{8}{x}$����kx2+2��2-k��x-8=0��
���б�ʽ��=0��4��2-k��2+32k=4��k+2��2=0����k=-2��
��ֱ��AB�ķ���Ϊy=-2x+8��
��x=0ʱ��y=8����y=0ʱ��x=4��
��A��0��8����B��4��0����
��AB=$\sqrt{64+16}=\sqrt{80}$=4$\sqrt{5}$��8944�ף�
���� ���⿼�麯����Ӧ�����⣬������ѧ֪ʶ���ʵ�����⣬����ѧ��������������������ȷ��������ϵ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
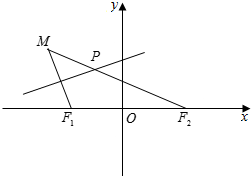 ��ͼ��ʾ����F1��-1��0����F2��1��0��������M����F2�ľ�����$2\sqrt{2}$���߶�MF1���д��߽�MF2�ڵ�P��
��ͼ��ʾ����F1��-1��0����F2��1��0��������M����F2�ľ�����$2\sqrt{2}$���߶�MF1���д��߽�MF2�ڵ�P���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{8}$ | B�� | $\frac{3}{8}$ | C�� | $\frac{5}{8}$ | D�� | $\frac{7}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �������� | C�� | �ڶ����� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 14 | B�� | 12 | C�� | 10 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
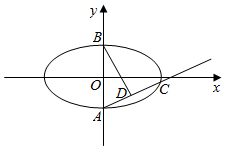 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲW��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{6}}{3}$������Բ�ҽ����Ҵ�ֱ��x���ֱ�߽���Բ���õ��ҵ��ҳ�Ϊ$\frac{2\sqrt{3}}{3}$������A��ֱ������ԲW������һ��C��
��ͼ����ƽ��ֱ������ϵxOy�У���ԲW��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{6}}{3}$������Բ�ҽ����Ҵ�ֱ��x���ֱ�߽���Բ���õ��ҵ��ҳ�Ϊ$\frac{2\sqrt{3}}{3}$������A��ֱ������ԲW������һ��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com