练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．函数f（x）的定义域为[-1，1]，图象如图1所示：函数g（x）的定义域为[-2，2]，图象如图2所示，方程f（g（x））=0有m个实数根，方程g（f（x））=0有n个实数根，则m+n=（　　）
    A．14B．12C．10D．8

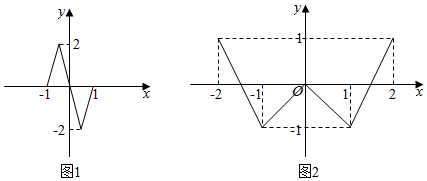
    分析 结合函数图象可知，若f（g（x））=0，则g（x）=-1或g（x）=0或g（x）=1；若g（f（x））=0，则f（x）=-1.5或f（x）=1.5或f（x）=0；从而再结合图象求解即可．

    解答 解：由图象可知，
    若f（g（x））=0，
    则g（x）=-1或g（x）=0或g（x）=1；
    由图2知，g（x）=-1时，x=-1或x=1；
    g（x）=0时，x的值有3个；
    g（x）=1时，x=2或x=-2；
    故m=7；
    若g（f（x））=0，
    则f（x）=-1.5或f（x）=1.5或f（x）=0；
    由图1知，
    f（x）=1.5与f（x）=-1.5各有2个；
    f（x）=0时，x=-1，x=1或x=0；
    故n=7；
    故m+n=14；
    故选：A．

    点评 本题考查了方程的根与函数的图象的关系应用及数形结合的思想应用，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

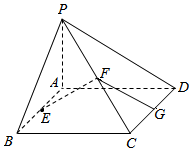    14．如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F、G分别是AB、PC、CD的中点，|PA|=|AB|=|AD|=1，
    （1）求证：EF∥平面PAD；
    （2）求证EF⊥CD，EF⊥PD，且|EF|=$\frac{1}{2}$|PD|；
    （3）求直线PD与AC所成的角；
    （4）求直线AP与平面PCD所成的角；
    （5）求平面PAB与平面PCD所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．某班有男、女优秀少先队员各2名，现需选出2名优秀少先队员到社区做公益宣传活动，则选出的两名队员性别相同的概率为（　　）
    A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{3}$，直线l：y=x+2与以原点O为圆心，椭圆的短半轴长为半径的圆O相切．
    （1）求椭圆C的方程；
    （2）设椭圆C与直线y=kx（k＞1）在第一象限的交点为A，B（$\sqrt{2}$，1），若$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\sqrt{6}$，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

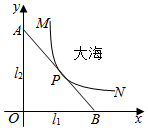    19．某沿海城市的海边有两条相互垂直的直线型公路l1、l2，海岸边界MPN近似地看成一条曲线段．为开发旅游资源，需修建一条连接两条公路的直线型观光大道AB，且直线AB与曲线MPN有且仅有一个公共点P（即直线与曲线相切），如图所示．若曲线段MPN是函数$y=\frac{a}{x}$图象的一段，点M到l1、l2的距离分别为8千米和1千米，点N到l2的距离为10千米，点P到l2的距离为2千米．以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy．
    （1）求曲线段MPN的函数关系式，并指出其定义域；
    （2）求直线AB的方程，并求出公路AB的长度（结果精确到1米）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=|x-1|-|x+2|．
    （1）求证：-3≤f（x）≤3；
    （2）求不等式：f（x）≥x2-2x-5的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知sin（α+$\frac{π}{3}$）=$\frac{1}{3}$，则sin（2α-$\frac{5π}{6}$）=$\frac{7}{9}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•（$\overrightarrow{a}$-$\overrightarrow{b}$）=2，且|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角等于$\frac{2π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设命题p：?x∈（0，+∞），$\sqrt{x}$≥log2x，则￢p为（　　）
    A．?x∈（0，+∞），$\sqrt{x}$≥log2xB．?x∈（0，+∞），$\sqrt{x}$＜log2xC．?x∈（0，+∞），$\sqrt{x}$=log2xD．?x∈（0，+∞），$\sqrt{x}$＜log2x

    查看答案和解析>>

    同步练习册答案