
分析 (1)根据绝对值的几何意义解不等式即可;
(2)通过讨论x的范围得到关于x的不等式组,解出取并集即可.
解答 解:(1)∵f(x)=|x-1|-|x+2|≤|(x-1)-(x+2)|=3,
∴-3≤f(x)≤3;
(2)x≤-2时,f(x)=1-x+x+2=3,原不等式等价于:
$\left\{\begin{array}{l}{3{≥x}^{2}-2x-5}\\{x≤-2}\end{array}\right.$,解得:x=-2,
-2<x<1时,f(x)=1-x-x-2=-2x-1,原不等式等价于:
$\left\{\begin{array}{l}{-2x-1{≥x}^{2}-2x-5}\\{-2<x<1}\end{array}\right.$,解得:-2<x<1,
x>1时,f(x)=x-1-x-2=-3,原不等式等价于:
$\left\{\begin{array}{l}{-3{≥x}^{2}-2x-5}\\{x≥1}\end{array}\right.$,解得:1≤x≤1+$\sqrt{3}$,
综上,不等式的解集是[-2,1+$\sqrt{3}$].
点评 本题考查了绝对值不等式的解法,考查绝对值的几何意义,是一道中档题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题
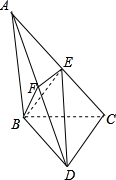 如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.
如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
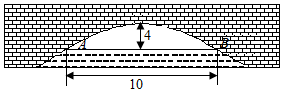 如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?
如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com