
| P��K2��k0�� | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
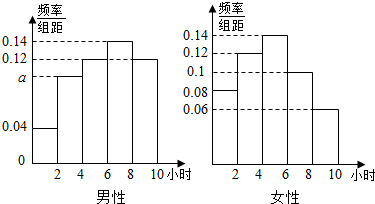
���� ��1������Ƶ�ʷֲ�ֱ��ͼ����Ů�������Եġ��ſء��롰���ſء���������д��������
����K2�����������ó����ʽ��ۣ�
��2�����÷ֲ����ԭ�������Ů����ѡ��5��ʱ���ſء��롰���ſء�������
��3�������оٷ���������¼����������Ӧ�ĸ���ֵ��
��� �⣺��1�������������ݣ�Ů��ʹ���ų���4Сʱ�������ǣ���0.14+0.1+0.06����2��50=30��
����4Сʱ��������20�ˣ�
����ʹ���ų���6Сʱ�������ǣ���0.12+0.14+0.12����2��50=38��
����6Сʱ��������12�ˣ�
��д�������ɵã�
| �ſ� | ���ſ� | �ϼ� | |
| ���� | 38 | 12 | 50 |
| �� | 30 | 20 | 50 |
| �ϼ� | 68 | 32 | 100 |
���� ���⿼���˶����Լ����Ӧ�����⣬Ҳ�����˷ֲ����������Ӧ����������оٷ���ŵ���͵ĸ������⣬�ǻ�����Ŀ��


 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
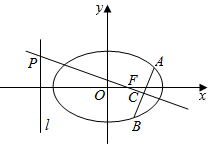 ��ͼ����ƽ��ֱ������ϵxOy�У���֪��Բ$\frac{x^2}{2}+{y^2}$=1���ҽ���F��ֱ��x=-2����F��ֱ������Բ����A��B���㣨AB��x���ֱ�����߶εĴ�ֱƽ���߷ֱ�ֱ��L��AB�ڵ�P��C����PC=2AB����ֱ��AB�ķ��̣�
��ͼ����ƽ��ֱ������ϵxOy�У���֪��Բ$\frac{x^2}{2}+{y^2}$=1���ҽ���F��ֱ��x=-2����F��ֱ������Բ����A��B���㣨AB��x���ֱ�����߶εĴ�ֱƽ���߷ֱ�ֱ��L��AB�ڵ�P��C����PC=2AB����ֱ��AB�ķ��̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | $\frac{7}{2}$ | C�� | 5 | D�� | $\frac{9}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com