
分析 由题意可得(2x+y)+y=2,整体代入可得$\frac{4}{2x+y}+\frac{1}{y}$=$\frac{1}{2}$(5+$\frac{4y}{2x+y}$+$\frac{2x+y}{y}$),由基本不等式可得.
解答 解:∵x>0,y>0,且x+y=1,
∴2x+2y=2,即(2x+y)+y=2,
∴$\frac{4}{2x+y}+\frac{1}{y}$=$\frac{1}{2}$($\frac{4}{2x+y}+\frac{1}{y}$)[(2x+y)+y]
=$\frac{1}{2}$(5+$\frac{4y}{2x+y}$+$\frac{2x+y}{y}$)≥$\frac{1}{2}$(5+2$\sqrt{\frac{4y}{2x+y}•\frac{2x+y}{y}}$)=$\frac{9}{2}$
当且仅当$\frac{4y}{2x+y}$=$\frac{2x+y}{y}$即2x+y=2y即y=2x=$\frac{2}{3}$时取等号.
故答案为:$\frac{9}{2}$.
点评 本题考查基本不等式求最值,整体代入并变形为可用基本不等式的形式是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
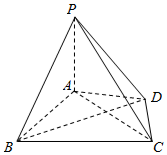 已知四棱锥P一ABCD,如图所示,其中平面PAD⊥平面ABCD,PA⊥AD,PA=AB=BC=AC=4,线段AC被线段BD平分.
已知四棱锥P一ABCD,如图所示,其中平面PAD⊥平面ABCD,PA⊥AD,PA=AB=BC=AC=4,线段AC被线段BD平分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
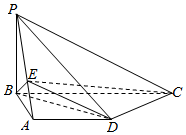 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,E是线段PA上一点,且$\frac{PE}{EA}$=λ.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,E是线段PA上一点,且$\frac{PE}{EA}$=λ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
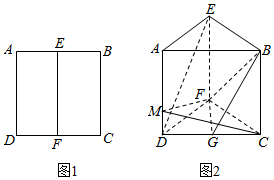 如图1,在边长为4的正方形ABCD中,E、F分别是AB、CD的中点,沿EF将矩形ADFE折起使得二面角A-EF-C的大小为90°(如图2),点G是CD的中点
如图1,在边长为4的正方形ABCD中,E、F分别是AB、CD的中点,沿EF将矩形ADFE折起使得二面角A-EF-C的大小为90°(如图2),点G是CD的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com