
分析 (1)化圆的一般式方程为标准式,由已知结合垂径定理求得m值;
(2)把圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$,转化为圆心到直线的距离d<1-$\frac{1}{\sqrt{5}}$,求解绝对值的不等式得答案.
解答 解:(1)圆的方程化为(x-1)2+(y-2)2=5-m,
圆心坐标为(1,2),半径为r=$\sqrt{5-m}$,
则圆心C(1,2)到直线l:x+2y-4=0的距离为d=$\frac{|1+2×2-4|}{\sqrt{{1}^{2}+{2}^{2}}}=\frac{1}{\sqrt{5}}$,
由于|MN|=$\frac{4}{\sqrt{5}}$,则$\frac{1}{2}|MN|$=$\frac{2}{\sqrt{5}}$,有${r}^{2}={d}^{2}+(\frac{1}{2}|MN|)^{2}$,
∴5-m=$(\frac{1}{\sqrt{5}})^{2}+(\frac{2}{\sqrt{5}})^{2}$,解得m=4;
(2)假设存在直线l:x-2y+c=0,使得圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$,
由于圆心C(1,2),半径r=1,则圆心C(1,2)到直线l:x-2y+c=0的距离为:
d=$\frac{|1-2×2+c|}{\sqrt{{1}^{2}+{2}^{2}}}=\frac{|c-3|}{\sqrt{5}}<|1-\frac{1}{\sqrt{5}}|$,
解得:$2+\frac{\sqrt{5}}{5}<c<4-\frac{\sqrt{5}}{5}$.
点评 本题考查直线与圆的位置关系,考查了点到直线距离公式的应用,考查绝对值不等式的解法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
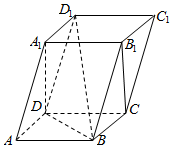 在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y=0 | B. | 2x+y-5=0 | C. | 2x+y-3=0 | D. | x-2y+4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
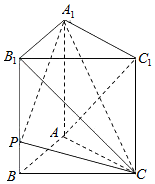 如图,已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.
如图,已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com