练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．若x，y满足不等式组$\left\{\begin{array}{l}{2x-3y-6≥0}\\{x+y-3≥0}\\{x≤a}\end{array}\right.$，z=x-y的最大值为4，则实数a=（　　）
    A．4B．$\frac{7}{2}$C．5D．$\frac{9}{2}$

    分析 作出可行域，变形目标函数，平移直线可得z的最值，可得a的方程，解方程可得．

    解答 解：作出不等式组$\left\{\begin{array}{l}{2x-3y-6≥0}\\{x+y-3≥0}\\{x≤a}\end{array}\right.$所对应可行域（如图△ABC），
    变形目标函数z=x-y可得y=x-z，平移直线y=x可知：
    当直线经过点A（a，3-a）时，直线截距最小值，z取最大值，
    代值可得a-（3-a）=4，解得a=$\frac{7}{2}$，
    故选：B．

    点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

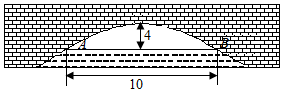    17．如图，一抛物线型拱桥的拱顶O离水面高4米，水面宽度AB=10米．现有一竹排运送一只货箱欲从桥下经过，已知货箱长20米，宽6米，高2.58米（竹排与水面持平），问货箱能否顺利通过该桥？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．微信是腾讯公司推出的一种手机通讯软件，它支持发送语音短信、视频、图片和文字，经推出便风靡全国，甚至涌现出一批在微信的朋友圈销售商的人（简称微商），为了调查每天微信用户使用微信的时间，某经销化妆品的微商在一广场随机采访男性、女性用户各50名，其中每天玩微信超过4小时的用户为“微信控”，否则称其为“非微信控”，调查结果如下：

    （1）根据以上数据，能否有60%的把握认为“微信控”与“性别”有关？
    （2）现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份，求所抽取5人中“微信控”与“非微信控”的人数；
    （3）从（2）中抽取的5人中在随机抽取2人赠送200元的护肤品套装，求这2人至少有1人为“非微信控”的概率．
    参考公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d．
    参数数据：
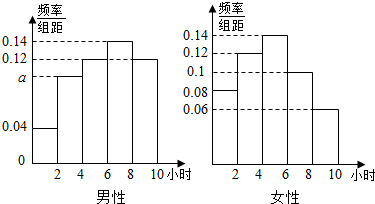
    P（K2≥k0）0.500.400.250.050.0250.010
    k00.4550.7081.3213.8405.0246.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．2015年山东省东部地区土豆种植形成初步规模，出口商在各地设置了大量的代收点．已知土豆收购按质量标准可分为四个等级，某代收点对等级的统计结果如下表所示：
    等级特级一级二级三级
    频率0.302mm0.10
    现从该代售点随机抽取了n袋土豆，其中二级品为恰有40袋．
    （Ⅰ）求m、n的值；
    （Ⅱ）利用分层抽样的方法从这n袋土豆中抽取10袋，剔除特级品后，再从剩余土豆中任意抽取两袋，求抽取的两袋都是一等品的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数y=f（x）是R上的偶函数，设a=ln$\frac{1}{π}$，b=（lnπ）2，c=ln$\sqrt{π}$，当任意x1、x2∈（0，+∞）时，都有（x1-x2）•[f（x1）-f（x2）]＜0，则（　　）
    A．f（a）＞f（b）＞f（c）B．f（b）＞f（a）＞f（c）C．f（c）＞f（b）＞f（a）D．f（c）＞f（a）＞f（b）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．定义在R上的函数f（x）满足f（x）=e2x+x2-ax，函数g（x）=f（$\frac{x}{2}$）-$\frac{1}{4}$x2+（1-b）x+b（其中a，b为常数），若函数f（x）在x=0处的切线与y轴垂直．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）求函数g（x）的单调区间；
    （Ⅲ）若s，t，r满足|s-r|＜|t-r|恒成立，则称s比t更靠近，在函数g（x）有极值的前提下，当x≥1时，$\frac{e}{x}$比ex-1+b更靠近，试求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．阅读如图所示的程序框图，运行相应的程序，则输出的n的值为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知圆C的方程：x2+y2-2x-4y+m=0．
    （1）若圆C与直线l：x+2y-4=0相交于M，N两点，且|MN|=$\frac{4\sqrt{5}}{5}$，求m的值；
    （2）在（1）条件下，是否存在直线l：x-2y+c=0，使得圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$，若存在，求出c的范围，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设n∈N+，a，b∈R，函数f（x）=$\frac{alnx}{x^n}$+b，己知曲线y=f（x）在点（1，0）处的切线方程为y=x-l．
    （I）求a，b；
    （Ⅱ）求f（x）的最大值；
    （Ⅲ）设c＞0且c≠l，已知函数g（x）=logcx-xn至少有一个零点，求c的最大值．

    查看答案和解析>>

    同步练习册答案