
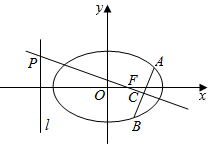
 如图,在平面直角坐标系xOy中,己知椭圆$\frac{x^2}{2}+{y^2}$=1的右焦点F,直线x=-2,过F的直线与椭圆交于A、B两点(AB与x轴不垂直),线段的垂直平分线分别交直线L和AB于点P、C.若PC=2AB,求直线AB的方程.
如图,在平面直角坐标系xOy中,己知椭圆$\frac{x^2}{2}+{y^2}$=1的右焦点F,直线x=-2,过F的直线与椭圆交于A、B两点(AB与x轴不垂直),线段的垂直平分线分别交直线L和AB于点P、C.若PC=2AB,求直线AB的方程. 分析 讨论直线AB的斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理和弦长公式,以及两直线垂直的条件和中点坐标公式,即可得到所求直线的方程.
解答 解:当AB⊥x轴,AB=$\sqrt{2}$,CP=3,不合题意;
当AB与x轴不垂直,设直线AB:y=k(x-1),A(x1,y1),B(x2,y2),
将AB方程代入椭圆方程可得(1+2k2)x2-4k2x+2(k2-1)=0,
则x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2({k}^{2}-1)}{1+2{k}^{2}}$,
则C($\frac{2{k}^{2}}{1+2{k}^{2}}$,$\frac{-k}{1+2{k}^{2}}$),
且|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$,
若k=0,则AB的垂直平分线为y轴,与左准线平行,不合题意;
则k≠0,故PC:y+$\frac{k}{1+2{k}^{2}}$=-$\frac{1}{k}$(x-$\frac{2{k}^{2}}{1+2{k}^{2}}$),P(-2,$\frac{2+5{k}^{2}}{k(1+2{k}^{2})}$),
从而|PC|=$\sqrt{1+\frac{1}{{k}^{2}}}$|xC-xP|=$\frac{2(3{k}^{2}+1)\sqrt{1+{k}^{2}}}{|k|(1+2{k}^{2})}$,
由|PC|=2|AB|,可得$\frac{2(3{k}^{2}+1)\sqrt{1+{k}^{2}}}{|k|(1+2{k}^{2})}$=$\frac{4\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$,
解得k=±1,
此时AB的方程为y=x-1或y=-x+1.
点评 本题考查椭圆的方程和性质,主要考查方程的运用,联立直线方程,运用韦达定理和弦长公式,同时考查两直线垂直和中点坐标公式的运用,属于中档题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
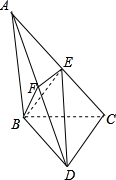 如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.
如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,5) | B. | -4 | C. | -4或20 | D. | -11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )
设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )| A. | {1} | B. | {2,4} | C. | {3,5} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
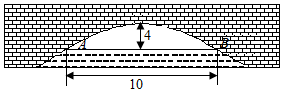 如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?
如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com