
分析 根据两角的关系进行转化2a-$\frac{5π}{6}$=2(α+$\frac{π}{3}$)-$\frac{3π}{2}$,再使用诱导公式化简.
解答 解:sin(2α-$\frac{5π}{6}$)=sin[2(α+$\frac{π}{3}$)-$\frac{3π}{2}$]
=sin[2($α+\frac{π}{3}$)+$\frac{π}{2}$]=cos2($α+\frac{π}{3}$)=1-2sin2($α+\frac{π}{3}$)
=1-2×($\frac{1}{3}$)2=$\frac{7}{9}$.
故答案为:$\frac{7}{9}$.
点评 本题考查了利用诱导公式化简三角函数,熟练掌握诱导公式是解题关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
 已知O为坐标原点,F为椭圆C:x2+$\frac{y^2}{2}$=1在y轴正半轴上的焦点,过F且斜率为-$\sqrt{2}$的直线l与C交与A、B两点,四边形OAPB为平行四边形.
已知O为坐标原点,F为椭圆C:x2+$\frac{y^2}{2}$=1在y轴正半轴上的焦点,过F且斜率为-$\sqrt{2}$的直线l与C交与A、B两点,四边形OAPB为平行四边形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
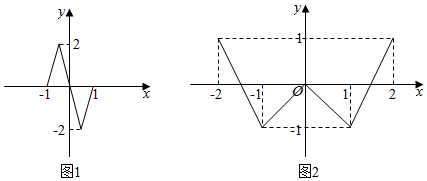
| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
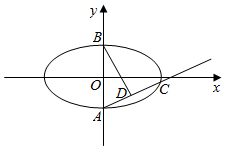 如图,在平面直角坐标系xOy中,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{6}}{3}$,过椭圆右焦点且垂直于x轴的直线交椭圆所得的弦的弦长为$\frac{2\sqrt{3}}{3}$,过点A的直线与椭圆W交于另一点C,
如图,在平面直角坐标系xOy中,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{6}}{3}$,过椭圆右焦点且垂直于x轴的直线交椭圆所得的弦的弦长为$\frac{2\sqrt{3}}{3}$,过点A的直线与椭圆W交于另一点C,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
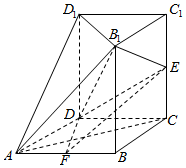 如图,几何体ABCD-B1C1D1中,四边形ABCD为菱形,∠BAD=60°,AB=a,平面B1C1D1∥平面ABCD,BB1、CC1、DD1都垂直于平面ABCD,且BB1=$\sqrt{2}$a,E为CC1的中点,F为AB的中点.
如图,几何体ABCD-B1C1D1中,四边形ABCD为菱形,∠BAD=60°,AB=a,平面B1C1D1∥平面ABCD,BB1、CC1、DD1都垂直于平面ABCD,且BB1=$\sqrt{2}$a,E为CC1的中点,F为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com