
 已知O为坐标原点,F为椭圆C:x2+$\frac{y^2}{2}$=1在y轴正半轴上的焦点,过F且斜率为-$\sqrt{2}$的直线l与C交与A、B两点,四边形OAPB为平行四边形.
已知O为坐标原点,F为椭圆C:x2+$\frac{y^2}{2}$=1在y轴正半轴上的焦点,过F且斜率为-$\sqrt{2}$的直线l与C交与A、B两点,四边形OAPB为平行四边形.分析 (Ⅰ)由已知F(0,1),直线l的方程为$y=-\sqrt{2}x+1$,代入${x^2}+\frac{y^2}{2}=1$,得$4{x^2}-2\sqrt{2}x-1=0$,由平行四边形性质得$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$,由此能证明点P在椭圆C上.
(Ⅱ)由已知求出|AB|和原点O到直线l:$y=-\sqrt{2}x+1$的距离,由此能求出四边形OAPB的面积.
解答 证明:(Ⅰ)∵O为坐标原点,F为椭圆C:x2+$\frac{y^2}{2}$=1在y轴正半轴上的焦点,
∴F(0,1),直线l的方程为$y=-\sqrt{2}x+1$,代入${x^2}+\frac{y^2}{2}=1$
并化简得$4{x^2}-2\sqrt{2}x-1=0$,…2分
设A(x1,y1),B(x2,y2),P(x3,y3),
∵四边形OAPB为平行四边形,∴$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$,…3分
可得(x3,y3)=(x1,y1)+(x2,y2)
∴${x_3}={x_1}+{x_2}=\frac{{\sqrt{2}}}{2}$,${y_3}={y_1}+{y_2}=-\sqrt{2}({x_1}+{x_2})+2=1$,故$P(\frac{{\sqrt{2}}}{2},1)$…5分
经验证点P的坐标$(\frac{{\sqrt{2}}}{2},1)$满足方程${x^2}+\frac{y^2}{2}=1$,
故点P在椭圆C上.…6分
解:(Ⅱ)∵$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\sqrt{3}\sqrt{{{(\frac{{\sqrt{2}}}{2})}^2}-4(-\frac{1}{4})}=\frac{3}{2}\sqrt{2}$…8分
原点O到直线l:$y=-\sqrt{2}x+1$的距离 $d=\frac{1}{{\sqrt{3}}}=\frac{{\sqrt{3}}}{3}$…10分
∴四边形OAPB的面积:
$S=2{S_{△OAB}}=|{AB}|•d=\frac{3}{2}\sqrt{2}•\frac{{\sqrt{3}}}{3}=\frac{{\sqrt{6}}}{2}$.…12分.
点评 本题考查点在椭圆上的证明,考查四边形面积的求法,解题时要注意圆锥曲线、椭圆性质、点到直线的距离公式的合理运用,是中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
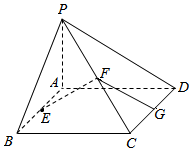 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F、G分别是AB、PC、CD的中点,|PA|=|AB|=|AD|=1,
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F、G分别是AB、PC、CD的中点,|PA|=|AB|=|AD|=1,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$) | B. | (0,$\frac{1}{2}$] | C. | ($\frac{1}{3}$,$\frac{1}{2}$] | D. | [$\frac{1}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
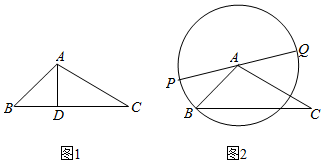 在△ABC中.
在△ABC中.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com