
分析 可求得f-1([0,2])=[$\frac{1}{ω}$(kπ-$\frac{5π}{6}$),$\frac{1}{ω}$(kπ+$\frac{π}{6}$)],(k∈Z),从而求得2sin(ωx+$\frac{5π}{6}$)∈[0,2],从而解得.
解答 解:由题意得,
f(x)=2sin(ωx+$\frac{5π}{6}$)(ω>0)的定义域为R,
f-1([0,2])={x|f(x)∈[0,2],x∈R},
故2sin(ωx+$\frac{5π}{6}$)∈[0,2];
故kπ≤ωx+$\frac{5π}{6}$≤kπ+π,k∈Z;
故$\frac{1}{ω}$(kπ-$\frac{5π}{6}$)≤x≤$\frac{1}{ω}$(kπ+$\frac{π}{6}$),k∈Z;
即f-1([0,2])=[$\frac{1}{ω}$(kπ-$\frac{5π}{6}$),$\frac{1}{ω}$(kπ+$\frac{π}{6}$)],(k∈Z);
故f(f-1([0,2]))
=f([$\frac{1}{ω}$(kπ-$\frac{5π}{6}$),$\frac{1}{ω}$(kπ+$\frac{π}{6}$)])
={y|y=f(x),x∈[$\frac{1}{ω}$(kπ-$\frac{5π}{6}$),$\frac{1}{ω}$(kπ+$\frac{π}{6}$)]},
故f(x)=2sin(ωx+$\frac{5π}{6}$)在[$\frac{1}{ω}$(kπ-$\frac{5π}{6}$),$\frac{1}{ω}$(kπ+$\frac{π}{6}$)]上的值域为[0,2];
∵x∈[$\frac{1}{ω}$(kπ-$\frac{5π}{6}$),$\frac{1}{ω}$(kπ+$\frac{π}{6}$)],
∴ωx∈[(kπ-$\frac{5π}{6}$),(kπ+$\frac{π}{6}$)],
∴ωx+$\frac{5π}{6}$∈[(kπ,(kπ+π)],
∴2sin(ωx+$\frac{5π}{6}$)∈[0,2].
故答案为:ω>0.
点评 本题考查了对应关系的应用及函数的定义域与值域的关系应用.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
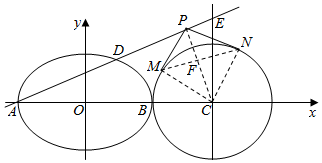 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A、B分别其左右顶点,直线AE交其右准线CE于点E,交椭圆于点D($\frac{1}{e}$,3),其中e为椭圆的离心率,B为线段OC的中点.圆C是以C点为圆心,CB长为半径的圆,P为直线AE上任意一点,过P向圆C作切线,切点分别为M、N.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A、B分别其左右顶点,直线AE交其右准线CE于点E,交椭圆于点D($\frac{1}{e}$,3),其中e为椭圆的离心率,B为线段OC的中点.圆C是以C点为圆心,CB长为半径的圆,P为直线AE上任意一点,过P向圆C作切线,切点分别为M、N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com