
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
已知数列{an}的相邻两项an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,且a1=1.
(1)求数列{ an}和{bn}的通项公式;
(2)设Sn是数列{an}的前n项的和,问是否存在常数λ,使得bn-λSn>0对任意n∈N*都成立,若存在,求出λ的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,下列命题为真命题的序号是
是两个不同的平面,下列命题为真命题的序号是
①若 ,则
,则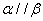 ;
;
②若 ,则
,则 ;
;
③若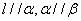 ,则
,则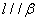 ;
;
④若 ,则
,则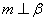 .
.
A.①④ B.①③ C.②④ D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为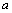 的平行线,将一根长度为
的平行线,将一根长度为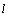 的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率
的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率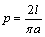 (
(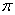 为圆周率).
为圆周率).
已知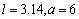 ,
,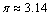 ,现随机掷14根相同的针(长度为
,现随机掷14根相同的针(长度为 )在这个平面上,记这些针与平行线(间距为
)在这个平面上,记这些针与平行线(间距为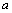 )相交的根数为
)相交的根数为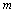 ,其相应的概率为
,其相应的概率为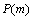 .当
.当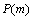 取得最大值时,
取得最大值时,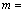 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com