
[ѡ����]��A��B��C��D��С����ֻ��ѡ�����⣬ÿС��10�֣�����20�֡����ڴ��ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�衣
A��ѡ��4 - 1������֤��ѡ��
��ͼ�����ı���ABCD�У���ABC�ա�BAD��
��֤��AB��CD��
B��ѡ��4 - 2��������任
����� �������
�������
C��ѡ��4 - 4������ϵ���������
��֪����C�IJ�������Ϊ ��
�� ������
Ϊ������ ����������C����ͨ���̡�
����������C����ͨ���̡�
D��ѡ��4 - 5������ʽѡ��
�� ��
�� ��0����֤��
��0����֤�� ��
�� ��
��
A��֤����������
B��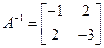
C��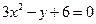
D��֤����������
����A����С����Ҫ�����ı��Ρ�ȫ�������ε��й�֪ʶ������������֤����������10�֡�
�ɡ�ABC�ա�BAD�á�ACB=��BDA����A��B��C��D�ĵ㹲Բ���Ӷ���CBA=��CDB�����ɡ�ABC�ա�BAD�á�CAB=��DBA����ˡ�DBA=��CDB������AB��CD��
B����С����Ҫ���������������������������������10�֡�
�����A�������Ϊ ����
����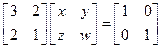 ��
��
��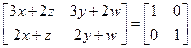 ����
����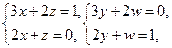 ��
��
��ã�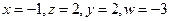 ��
��
�Ӷ�A�������Ϊ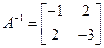 ��
��
C����С����Ҫ����������̺���ͨ���̵Ļ���֪ʶ������ת�����������������10�֡�
��Ϊ ������
������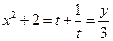 ��
��
������C����ͨ����Ϊ��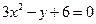 ��
��
D����С����Ҫ����ȽϷ�֤������ʽ�ij����������������ʽ�ı�������������10�֡�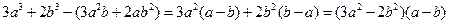 ��
��
��Ϊ ��
�� ��0������
��0������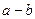 ��0��
��0��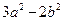 ��0���Ӷ�
��0���Ӷ� ��0��
��0��
�� ��
�� ��
��


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ѡ���⣩��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����ڴ��ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裮
��ѡ���⣩��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����ڴ��ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裮| 3 |
| 3 |
|
| 2 |
| �� |
| 4 |
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ѡ���⣺��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣���20�֣����Ӧд������˵����֤�����̻����㲽�裮
ѡ���⣺��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣���20�֣����Ӧд������˵����֤�����̻����㲽�裮
|
|
| 2 |
| �� |
| 4 |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ѡ���⣨��A��B��C��D��С����ֻ��ѡ�����⣬����ѡ�������2BǦ��Ϳ�ڣ�ÿС��10�֣���20�֣����ڴ���ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裩��
ѡ���⣨��A��B��C��D��С����ֻ��ѡ�����⣬����ѡ�������2BǦ��Ϳ�ڣ�ÿС��10�֣���20�֣����ڴ���ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裩��
|
| �� |
| 4 |
| ||
| 2 |
| ab |
| bc |
| ca |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

|
|
| 1 |
| b |
| 1 |
| 2a |
| 9 |
| 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com