已知点A.B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1上两点.F1.F2为椭圆的左右焦点.且满足AF1∥BF2.AF2与BF1交于点P．记∠AF1x=α．(1)求证:|AF1|=$\frac{{b}^{2}}{a-ccosα}$.|BF2|=$\frac{{b}^{2}}{a+ccosα}$,(2)当A.B在椭圆上移� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

8．已知点A，B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上两点，F₁，F₂为椭圆的左右焦点，且满足AF₁∥BF₂，AF₂与BF₁交于点P．记∠AF₁x=α．
（1）求证：|AF₁|=$\frac{{b}^{2}}{a-ccosα}$，|BF₂|=$\frac{{b}^{2}}{a+ccosα}$；
（2）当A，B在椭圆上移动时，求证：动点P的轨迹也是一个椭圆；
（3）将（1）（2）的结论推广到双曲线，并证明你的结论．

分析（1）如图所示，设|AF₁|=m，|AF₂|=2a-m，在△AF₁F₂，由余弦定理即可得出|AF₁|，同理可得：|BF₂|；
（2）由AF₁∥BF₂，可得$\frac{BP}{P{F}_{1}}=\frac{B{F}_{2}}{A{F}_{1}}$，于是$P{F}_{1}=\frac{A{F}_{1}}{B{F}_{2}+A{F}_{1}}B{F}_{1}$=$\frac{A{F}_{1}}{B{F}_{2}+A{F}_{1}}（2a-B{F}_{2}）$，同理可得：PF₂=$\frac{B{F}_{2}}{B{F}_{2}+A{F}_{1}}（2a-A{F}_{1}）$，可得PF₁+PF₂═$\frac{{a}^{2}+{c}^{2}}{a}$＞2c，即可证明．
（3）类比（2）利用平行线的性质与双曲线的定义及其性质即可证明．

解答（1）证明：如图所示，
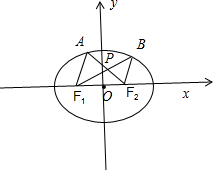
设|AF₁|=m，|AF₂|=2a-m，
在△AF₁F₂，由余弦定理可得：（2a-m）²=m²+4c²-2m•2ccosα，
化为：$m=\frac{{b}^{2}}{a-ccosα}$=|AF₁|，
同理可得：|BF₂|=$\frac{{b}^{2}}{a+ccosα}$；
（2）证明：∵AF₁∥BF₂，∴$\frac{BP}{P{F}_{1}}=\frac{B{F}_{2}}{A{F}_{1}}$，
∴$\frac{B{F}_{1}}{P{F}_{1}}=\frac{B{F}_{2}+A{F}_{1}}{A{F}_{1}}$，
∴$P{F}_{1}=\frac{A{F}_{1}}{B{F}_{2}+A{F}_{1}}B{F}_{1}$=$\frac{A{F}_{1}}{B{F}_{2}+A{F}_{1}}（2a-B{F}_{2}）$，
同理可得：PF₂=$\frac{A{F}_{2}}{B{F}_{2}+A{F}_{1}}B{F}_{2}$=$\frac{B{F}_{2}}{B{F}_{2}+A{F}_{1}}（2a-A{F}_{1}）$，
∴PF₁+PF₂=2a-$\frac{2A{F}_{1}•B{F}_{2}}{B{F}_{2}+A{F}_{1}}$=2a-$\frac{\frac{2{b}^{2}}{a-ccosα}•\frac{{b}^{2}}{a+ccosα}}{\frac{{b}^{2}}{a-ccosα}+\frac{{b}^{2}}{a+ccosα}}$=2a-$\frac{{b}^{2}}{a}$=$\frac{{a}^{2}+{c}^{2}}{a}$＞2c，
∴动点P的轨迹也是一个椭圆，焦点仍然为F₁，F₂，中心为原点O，长轴长为$\frac{{a}^{2}+{c}^{2}}{a}$（＜2a）．
（3）解：对于双曲线：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a，b＞0），可得：
（i）|BF₂|=$\frac{{b}^{2}}{a-ccosα}$，|AF₁|=$\frac{{b}^{2}}{a+ccosα}$．
（ii）当A，B在双曲线上移动时，动点P的轨迹也是双曲线．
类比（2）利用平行线的性质与双曲线的定义及其性质即可证明．

点评本题考查了椭圆与双曲线的标准方程及其性质、平行线的性质，考查了类比推理能力与计算能力，属于难题．

练习册系列答案

暑假作业教育科学出版社系列答案

新课标暑假作业二十一世纪出版社系列答案

暑假作业期末综合复习东南大学出版社系列答案

书香天博暑假作业西安出版社系列答案

暑假作业江苏人民出版社系列答案

新浪书业复习总动员年度总复习精要暑长江出版社系列答案

假期新观察安徽科学技术出版社系列答案

暑假新动向电子科技大学出版社系列答案

暑假生活微指导四川师范大学电子出版社系列答案

高考大突破黄金考卷绿色假期暑假作业新世纪出版社系列答案