
| Sn |
| S2n |
| 4 | ||
|
| 1 | ||
|
| Sn |
| S2n |
|
| 4 | ||
|
| 1 | ||
|
| 4 |
| k |
| 1 |
| h |
| 1 |
| 2013 |
| 4 |
| k |
| 1 |
| h |
| Sn |
| S2n |
| ||
|
| 1 |
| 4 |
| Sn |
| S2n |
|
| 1 |
| 4 |
| 4 | ||
|
| 1 | ||
|
| 4 |
| k |
| 1 |
| h |
| 1 |
| 2013 |
| 4 |
| k |
| 1 |
| h |
| 1 |
| 2013 |
| k |
| h |
| 4h |
| k |
| 1 |
| 2013 |
| 3 |
| 671 |
| 4 | ||
|
| 1 | ||
|
| 3 |
| 671 |


科目:高中数学 来源: 题型:
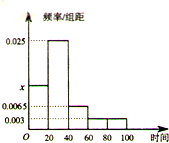 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 在△ABC中,已知
在△ABC中,已知| AB |
| AC |
| AP |
| ||
|
|
| ||
|
|
| 2 |
| x |
| 1 |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:
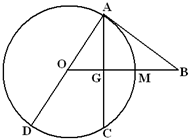 如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.
如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.| 3 |
| 5 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 非统计专业 | 统计专业 | |
| 男生 | 14 | 10 |
| 女生 | 6 | 20 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com