
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量![]() =(a,
=(a,![]() b)与
b)与![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(1)求A;
(2)若a=![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,点
轴非负半轴为极轴建立极坐标系,点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 面积的最小值。
面积的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其最小正周期为
,其最小正周期为![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长到原来的
个单位长度后,再将得到的图象上各点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由线性回归方程得到的估计数据与4月份所选5天的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的. 请根据4月7日,4月15日与4月21日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判定所得的线性回归方程是否可靠?
,并判定所得的线性回归方程是否可靠?
参考公式: 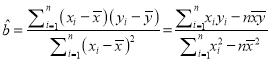 ,
, ![]()
参考数据: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下表格记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以![]() 表示.
表示.
甲组 | 9 | 9 | 11 | 11 |
乙组 |
| 8 | 9 | 10 |
(1)如果![]() ,求乙组同学植树棵数的平均数和方差;
,求乙组同学植树棵数的平均数和方差;
(2)如果![]() ,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com