
分析 (1)根据向量的坐标表示求得$\overrightarrow{a}$-$\overrightarrow{b}$,由模长公式可知$\sqrt{2-2cos(α-β)}$=$\frac{\sqrt{10}}{5}$,即可求得cos(α-β)的值;
(2)由-$\frac{π}{2}$<α<0,0<β<$\frac{π}{2}$,求得-π<α-β<0,由同角三角函数基本关系求得sin(α-β)及sinα的值,cosβ=cos[α-(α-β)],根据两角和的余弦公式即可即可求得cosβ的值.
解答 解:(1)$\overrightarrow{a}$-$\overrightarrow{b}$=(cosα-cosβ,sinα-sinβ),
丨$\overrightarrow{a}$-$\overrightarrow{b}$丨=$\sqrt{(cosα-cosβ)^{2}+(sinα-sinβ)^{2}}$,
=$\sqrt{2-2(cosαcosβ+sinαsinβ)}$,
=$\sqrt{2-2cos(α-β)}$,
2-2cos(α-β)=$\frac{2}{5}$,
∴cos(α-β)=$\frac{4}{5}$;
(2)∵-$\frac{π}{2}$<α<0,0<β<$\frac{π}{2}$,
∴-π<α-β<0,
∴sin(α-β)<0,sin(α-β)=-$\sqrt{1-co{s}^{2}(α-β)}$=-$\frac{3}{5}$,
$cosα=\frac{12}{13}$,sinα=-$\sqrt{1-co{s}^{2}α}$=-$\frac{5}{13}$,
cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β),
=$\frac{12}{13}$×$\frac{4}{5}$+(-$\frac{5}{13}$)×(-$\frac{3}{5}$)
=$\frac{63}{65}$,
∴cosβ=$\frac{63}{65}$.
点评 本题考查两角和差余弦公式,向量的坐标表示、模长公式及同角三角函数基本关系,考查计算能力,属于中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | ±8 | D. | ±4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
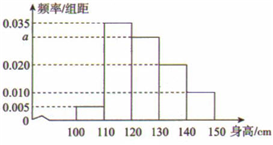 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动.
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com