
���� �������⣬���оٷ��ɵ����п��ܵİͨ��˳�������������ɵ�С�������ŵȳ��������Ŀ���ɵȿ����¼��ĸ��ʹ�ʽ������ɵô𰸣�
��� �⣺�������⣬���п��ܵİͨ��˳������Ϊ���š��С�������š���У������С��š�������С���ţ�������У��ţ�������ţ��У�����6�֣�
����С�������ŵȳ�������У��С��š�������С���ţ�������ţ��У�����3�֣�
�������Ϊ$\frac{1}{2}$
�ʴ�Ϊ$\frac{1}{2}$
���� ���⿼��ȿ����¼��ĸ��ʼ��㣬�ؼ������оٷ��������ͨ����ȫ��˳������Գ����ŵȳ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ڵ�ʮ����������˻��ϣ�ij��Ŀ�ı�������Ϊ�������ˣ���Ϊ���ң����б�����ÿ��ʤ�ߵ�1�֣����ߵ�0�֣���ƽ�֣����������е���һ�˱ȶԷ���2�ֻ����6��ʱֹͣ�������ÿ���л�ʤ�ĸ���Ϊp��p��0.5�����Ҹ���ʤ�����������֪�ڶ��ֱ�������ʱ����ֹͣ�ĸ���Ϊ$\frac{5}{9}$��
�ڵ�ʮ����������˻��ϣ�ij��Ŀ�ı�������Ϊ�������ˣ���Ϊ���ң����б�����ÿ��ʤ�ߵ�1�֣����ߵ�0�֣���ƽ�֣����������е���һ�˱ȶԷ���2�ֻ����6��ʱֹͣ�������ÿ���л�ʤ�ĸ���Ϊp��p��0.5�����Ҹ���ʤ�����������֪�ڶ��ֱ�������ʱ����ֹͣ�ĸ���Ϊ$\frac{5}{9}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�갲������һ�и߶�������ĩ�������ѧ�Ծ��������棩 ���ͣ������
��ij�������и���������һ̨�磬�ݼ�⣬��ǰ̨������λ�ڳ��� ����ͼ���Ķ�ƫ��
����ͼ���Ķ�ƫ�� ����300km�ĺ���
����300km�ĺ��� ��������20km/h���ٶ�����ƫ��
��������20km/h���ٶ�����ƫ�� �����ƶ���̨����Ϯ�ķ�ΧΪԲ������ǰ�뾶Ϊ60km������10km/h���ٶȲ��������ʼ�Сʱ��ó��п�ʼ�ܵ�̨�����Ϯ���ܵ�̨����Ϯ��ʱ���ж���Сʱ��
�����ƶ���̨����Ϯ�ķ�ΧΪԲ������ǰ�뾶Ϊ60km������10km/h���ٶȲ��������ʼ�Сʱ��ó��п�ʼ�ܵ�̨�����Ϯ���ܵ�̨����Ϯ��ʱ���ж���Сʱ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�갲������һ�и߶�������ĩ�������ѧ�Ծ��������棩 ���ͣ�ѡ����
������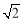 ��
�� ��
�� ��
�� ��
�� ����������
���������� ��������еĵڣ� ����
��������еĵڣ� ����
A��8 B��9 C��10 D��11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������PBC����Բ��O��PB=OB=1��OB�Ƶ�O��ʱ����$\frac{2��}{3}$��OD����PD��ԲO�ڵ�E����PE=$\frac{3\sqrt{7}}{7}$��
��ͼ������PBC����Բ��O��PB=OB=1��OB�Ƶ�O��ʱ����$\frac{2��}{3}$��OD����PD��ԲO�ڵ�E����PE=$\frac{3\sqrt{7}}{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�����Σ��ı���CDEF�Ǿ��Σ���ƽ��ABCD��ƽ��CDEF����BAD=��CDA=90�㣬AB=AD=DE=CD=2��M���߶�AE�ϵĶ��㣮
��ͼ���ı���ABCD�����Σ��ı���CDEF�Ǿ��Σ���ƽ��ABCD��ƽ��CDEF����BAD=��CDA=90�㣬AB=AD=DE=CD=2��M���߶�AE�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b��2 | B�� | b��5 | C�� | b��2 | D�� | b��5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com