
分析 (1)当k=0时,求函数的导数,利用函数的单调性和导数之间的关系即可求f(x)的单调区间;
(2)若x≥0时,f(x)≥0恒成立,求函数导数,讨论k的范围,结合函数的单调性研究最值即可求k的取值范围.
解答 解:(1)当k=0时,f(x)=e2x-1-2x,f'(x)=2e2x-2,…(1分)
令f'(x)>0,则2e2x-2>0,解得:x>0,
令f'(x)<0,则2e2x-2<0,解得:x<0,…(3分)
所以,函数f(x)=e2x-1-2x的单调增区间为(0,+∞),
单调减区间为(-∞,0). ….(4分)
(2)由函数f(x)=e2x-1-2x-kx2,
则f'(x)=2e2x-2kx-2=2(e2x-kx-1),
令g(x)=e2x-kx-1,则g'(x)=2e2x-k. …(6分)
由x≥0,所以,
①当k≤2时,g'(x)≥0,g(x)为增函数,而g(0)=0,
所以g(x)≥0,即f'(x)≥0,所以f(x)在[0,+∞)上为增函数,
而f(0)=0,所以f(x)≥0在[0,+∞)上恒成立. …(9分)
②当k>2时,令g'(x)<0,即2e2x-k<0,则$0≤x<\frac{1}{2}ln\frac{k}{2}$.
即g(x)在$[{0,\frac{1}{2}ln\frac{k}{2}}]$上为减函数,而g(0)=0,所以,g(x)在$[{0,\frac{1}{2}ln\frac{k}{2}}]$上小于0.即f'(x)<0,
所以f(x)在$[{0,\frac{1}{2}ln\frac{k}{2}}]$上为减函数,而f(0)=0,故此时f(x)<0,不合题意.
综上,k≤2. …(12分)
点评 本题主要考查函数单调性的判断以及不等式恒成立的应用,求函数的导数,利用函数单调性和导数之间的关系进行判断是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
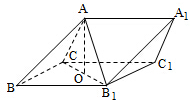 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
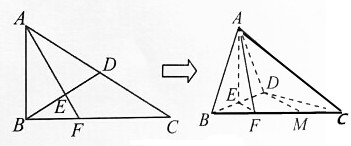 如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.
如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
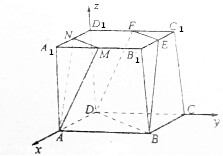 如图,正方体ABCD-A1B1C1D1的棱长为a,点M、N、E、F分别是A1B1、A1D1、B1C1、C1D1的中点,则点M到平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;直线AM与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;平面AMN与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$.
如图,正方体ABCD-A1B1C1D1的棱长为a,点M、N、E、F分别是A1B1、A1D1、B1C1、C1D1的中点,则点M到平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;直线AM与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;平面AMN与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
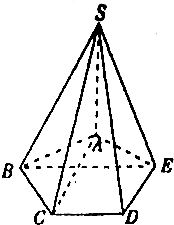 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com