
分析 由条件可得,(x-b){(1-3m)x2+[m(2a+b)-(a+b)]x+ab}≥0恒成立,可得m=$\frac{1}{3}$,故(x-b)[(a+2b)x-3ab]≤0恒成立.再利用二次函数的性质求出a-b=0即可.
解答 解:∵f(x)≥mxf′(x),
∴(x-a)(x-b)2 ≥m•x(x-b)[3x-(2a+b)],
∴(x-b){(1-3m)x2+[m(2a+b)-(a+b)]x+ab}≥0.
若m≠$\frac{1}{3}$,则左边是一个一次因式,乘以一个恒正(或恒负)的二次三项式,或者是三个一次因式的积,无论哪种
情况,总有一个一次因式的指数是奇次的,这个因式的零点左右的符号不同,因此不可能恒非负,不满足条件.
∴m=$\frac{1}{3}$,
∴(x-b)[(a+2b)x-3ab]≤0恒成立.
若a+2b=0,则有a=-2b,∴a=b=0,(舍)
若a+2b≠0,则 x1=b,x2=$\frac{3ab}{a+2b}$,且 b=$\frac{3ab}{a+2b}$.
∵b≠0,则 $\frac{3a}{a+2b}$=1,∴a=b,即a-b=0且b<0.
综上可得,m=$\frac{1}{3}$,a-b=0,
∴2m+a-b=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题主要考查函数在某点取得极值的条件,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
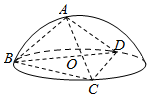 如图,半球O内有一内接正三棱锥A-BCD(底面△BCD为等边三角形,顶点A在底面的射影为ABCD的中心),且△BCD内接于圆O,当半球O的体积为2$\sqrt{3}$π时,三棱锥A-BCD的所有棱长之和为9+3$\sqrt{6}$.
如图,半球O内有一内接正三棱锥A-BCD(底面△BCD为等边三角形,顶点A在底面的射影为ABCD的中心),且△BCD内接于圆O,当半球O的体积为2$\sqrt{3}$π时,三棱锥A-BCD的所有棱长之和为9+3$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
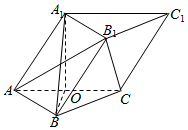 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC=$\frac{π}{3}$,点O为AC的中点.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC=$\frac{π}{3}$,点O为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{2}$] | B. | (-∞,1) | C. | [$\frac{1}{2}$,1) | D. | (-1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com