
分析 将函数化为f(x)=-sin2x+2asinx,令t=sinx,t∈[0,1],化函数y=f(x)=-t2+2at=-(t-a)2+a2,求出对称轴,讨论区间与对称轴的关系,结合单调性,即可得到所求最大值.
解答 解:函数f(x)=cos2x+2asinx-1
=-sin2x+2asinx,
令t=sinx,
由x∈[0,$\frac{π}{2}$],可得t=sinx∈[0,1],
则函数y=f(x)=-t2+2at=-(t-a)2+a2,
对称轴t=a,
当a≥1时,函数y在[0,1]递增,可得t=1时,取得最大值2a-1;
当a≤0时,函数y在[0,1]递减,可得t=0时,取得最大值0;
当0<a<1时,函数y在t=a处取得最大值,且为a2.
综上可得,当a≥1时,函数的最大值为2a-1;
当a≤0时,函数的最大值为0;
当0<a<1时,函数的最大值为a2.
点评 本题考查函数的最值的求法,注意运用换元法化为二次函数在闭区间上的最值,考查分类讨论的思想方法,属于中档题.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:选择题
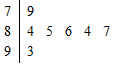 如图是巴蜀中学“高2017级跃动青春自编操”比赛上,七位评委为某班打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
如图是巴蜀中学“高2017级跃动青春自编操”比赛上,七位评委为某班打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )| A. | 84,84 | B. | 84,85 | C. | 85,84 | D. | 85,85 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,$\frac{π}{2}$) | B. | (3,-$\frac{π}{2}$) | C. | (3,0) | D. | (3,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
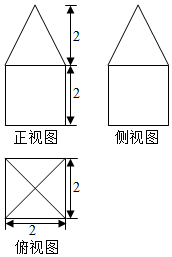
| A. | 8 cm3 | B. | 12 cm3 | C. | $\frac{32}{3}$ cm3 | D. | $\frac{40}{3}$ cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
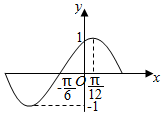 如图是函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的一段图象,则函数的解析式为y=sin(2x+$\frac{π}{3}$).
如图是函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的一段图象,则函数的解析式为y=sin(2x+$\frac{π}{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com