
分析 (1)根据抽象函数的关系,利用赋值法进行求解.
(2)令x=$\frac{k}{n}$,则f($\frac{k}{n}$)+f($\frac{n-k}{n}$)=2,利用倒序相加法进行求和,结合等差数列的定义进行证明.
(3)求出数列{bn}的通项公式,根据数列的递推关系进行转化求解即可.
解答 解:(1)f(x)对任意x∈R都有f(x)+f(1-x)=2.
∴当x=$\frac{1}{2}$时,f($\frac{1}{2}$)+f(1-$\frac{1}{2}$)=2=2f($\frac{1}{2}$).
则f($\frac{1}{2}$)=1,
令x=$\frac{1}{n}$,则f($\frac{1}{n}$)+f(1-$\frac{1}{n}$)=2,即f($\frac{1}{n}$)+f($\frac{n-1}{n}$)=2,
(2)证明:f(x)对任意x∈R都有f(x)+f(1-x)=2.
则令x=$\frac{k}{n}$,则f($\frac{k}{n}$)+f($\frac{n-k}{n}$)=2,
∵${a_n}=f(0)+f(\frac{1}{n})+f(\frac{2}{n})+…+f(\frac{n-1}{n})+f(1)$,
∴an=f(1)+f($\frac{n-1}{n}$)+f($\frac{n-2}{n}$)+…+f($\frac{1}{n}$)+f(0),
则两式相加得2an=[f(0)+f(1)]+[f($\frac{1}{n}$)+f($\frac{n-1}{n}$)]+…+f($\frac{n-2}{n}$)+…+[f(1)+f(0)]=2(n+1),
则an=n+1,
则an+1-an=n+2-(n+1)=1,为常数,
∴{an}是等差数列.
(3)bn=$\frac{1}{{{a_n}-1}}$=$\frac{1}{n}$,则易知T2n-Tn=$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{2n}$=f(n),
则f(n+1)-f(n)=$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{2n+2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$-$\frac{1}{n+3}$-…-$\frac{1}{2n}$=$\frac{1}{2n+1}$+$\frac{1}{2n+2}$-$\frac{1}{n+1}$=$\frac{1}{2n+1}$-$\frac{1}{2n+2}$>0
所以f(n)单调递增.
所以T2n-Tn≥f(2)=$\frac{1}{3}+\frac{1}{4}$=$\frac{7}{12}$,
故$\frac{7}{12}$>$\frac{7}{12}(1+{log_{a+1}}x-{log_a}x)$
所以loga+1x<logax,
于是$\frac{lgx}{lg(a+1)}$<$\frac{lgx}{lga}$,(a>0,lga>0)恒成立
于是x>1.
点评 本题主要考查抽象函数以及数列和不等式的综合以及不等式恒成立问题,利用赋值法以及转化法是解决本题的关键.综合性较强,运算量较大,有一定的难度.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
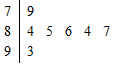 如图是巴蜀中学“高2017级跃动青春自编操”比赛上,七位评委为某班打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
如图是巴蜀中学“高2017级跃动青春自编操”比赛上,七位评委为某班打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )| A. | 84,84 | B. | 84,85 | C. | 85,84 | D. | 85,85 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com