考点:命题的真假判断与应用
专题:函数的性质及应用
分析:由函数的奇偶性的定义,即可判断①;运用函数的周期性,即可判断②;画出y=x
2,y=2
x的图象,注意f(2)=0,f(4)=0,从而判断③;作出y=|log
2x|和y=(
)
x在(0,+∞)上的图象,结合图象判断交点个数和范围,即可判断④.
解答:
解:①函数y=2
-|x|为偶函数,由于f(-x)=2
-|-x|=2
-|x|=f(x),
故①正确;
②函数y=1,即f(x)=1,存在非零常数T,有f(x+T)=f(x),
故为周期函数,即②正确;
③函数f(x)=2
x-x
2的零点,即令f(x)=0,2
x=x
2,
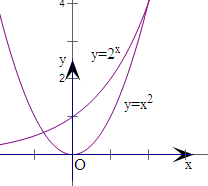
显然有f(2)=0,f(4)=0,当x<0时,y=x
2递减,
y=2
x递增,显然有一个交点,故有三个交点,故③错;
④令g(x)=0,则|log
2x|=(
)x,
作出y=|log
2x|和y=(
)
x在(0,+∞)上的图象,
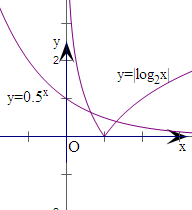
可知恰有两个交点,设零点为x
1,x
2且
|log
2x
1|>|log
2x
2|,x
1<1,x
2>1,
故有
>x2,即x
1x
2<1,故④正确.
故选C.
点评:本题主要考查函数的奇偶性和周期性及运用,考查函数的零点个数的判断,掌握运用图象求交点个数,注意运用数形结合思想,是一道中档题.

 解:①函数y=2-|x|为偶函数,由于f(-x)=2-|-x|=2-|x|=f(x),
解:①函数y=2-|x|为偶函数,由于f(-x)=2-|-x|=2-|x|=f(x),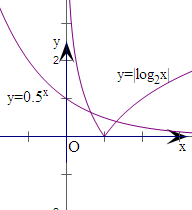


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=
如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=