
分析 化简等式可得sin(ωx0+2ω+φ)-sin(ωx0+φ)=2,由正弦函数的性质可求ω=(k1-k2)π-$\frac{π}{2}$,k1、k2∈Z,结合ω>0求得ω的最小值.
解答 解:存在x0∈R,使得f(x0+2)-f(x0)=4,
即2sin[ω(x0+2)+φ]-2sin(ωx0+φ)=4成立,
∴sin(ωx0+2ω+φ)-sin(ωx0+φ)=2,
∴ωx0+2ω+φ=2k1π+$\frac{π}{2}$①,
ωx0+φ=2k2π+$\frac{3π}{2}$②,k1、k2∈Z;
由①②解得:ω=k1π-k2π-$\frac{π}{2}$,k1、k2∈Z;
又ω>0,∴ω的最小值是$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题主要考查了正弦函数的图象和性质以及特殊角的三角函数值应用问题,属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | |||
| 学习积极性一般 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费x(万元) | 1 | 2 | 3 | 4 | 5 |
| 销售量y(万台) | 2 | 5 | 10 | 15 | 18 |
| A. | 30 | B. | 52 | C. | 57.2 | D. | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{20}{3}$ | B. | $\frac{40}{3}$ | C. | $\frac{8}{3}$ | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
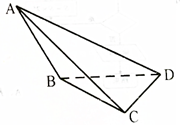 如图所示,在三棱锥A-BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边且AD=$\sqrt{3}$,BD=CD=1,另一侧面ABC是正三角形.
如图所示,在三棱锥A-BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边且AD=$\sqrt{3}$,BD=CD=1,另一侧面ABC是正三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com