
| 广告费x(万元) | 1 | 2 | 3 | 4 | 5 |
| 销售量y(万台) | 2 | 5 | 10 | 15 | 18 |
| A. | 30 | B. | 52 | C. | 57.2 | D. | 70 |
分析 由表中数据计算$\overline{x}$、$\overline{y}$,由回归方程过样本中心($\overline{x}$,$\overline{y}$)求出$\stackrel{∧}{a}$,写出回归方程,利用回归方程计算x=13时$\stackrel{∧}{y}$的值即可.
解答 解:由表中数据可得,$\overline{x}$=$\frac{1}{5}$×(1+2+3+4+5)=3,
$\overline{y}$=$\frac{1}{5}$×(2+5+10+15+18)=10
而回归方程经过样本中心($\overline{x}$,$\overline{y}$),且$\stackrel{∧}{b}$=4.2,
∴$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=10-4.2×3=-2.6,
∴回归方程是$\stackrel{∧}{y}$=4.2x-2.6,
∴当x=13时,$\stackrel{∧}{y}$=4.2×13-2.6=52(万台).
故选:B.
点评 本题考查了回归直线方程的应用问题,利用回归直线方程过样本中心点是关键,属于基础题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
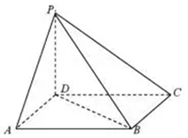 如图,四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 认为作业多 | 认为作业少 | 总计 | |
| 喜欢玩电脑游戏 | 10 | 35 | 45 |
| 不喜欢玩玩电脑游戏 | 7 | 38 | 45 |
| 总计 | 17 | 73 | 90 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 |
| A. | 0.15~0.25 | B. | 0.4~0.5 | C. | 0.5~0.6 | D. | 0.75~0.85 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$i | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{2}$i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com