
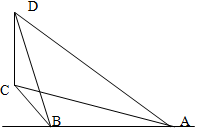
 一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15.的方向上,行驶5km后到达B处,测得此山顶在西偏北45.的方向上,此时看山顶的仰角为30,求此山CD的高.
一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15.的方向上,行驶5km后到达B处,测得此山顶在西偏北45.的方向上,此时看山顶的仰角为30,求此山CD的高. 分析 在△ABC中,利用正弦定理计算BC,再在Rt△BCD中求出CD.
解答 解:由题意可知AB=5,∠CAB=15°,∠ABC=135°,∠DBC=30°,
∴∠ACB=30°,
在△ABC中,由正弦定理得:$\frac{AB}{sin∠ACB}=\frac{BC}{sin∠BAC}$,
∴BC=$\frac{AB•sin∠CAB}{sin∠ACB}$=$\frac{5sin15°}{sin30°}$=10sin15°=$\frac{5(\sqrt{6}-\sqrt{2})}{2}$,
在Rt△BCD中,∵$\frac{CD}{BC}$=tan∠DBC=$\frac{\sqrt{3}}{3}$,
∴CD=$\frac{\sqrt{3}}{3}$BC=$\frac{\sqrt{3}}{3}×$$\frac{5(\sqrt{6}-\sqrt{2})}{2}$=$\frac{5\sqrt{2}}{2}$-$\frac{5\sqrt{6}}{6}$.
点评 本题考查了正弦定理,解三角形的实际应用,属于基础题.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:填空题
| 死亡 | 存活 | 总计 | |
| 第一种剂量 | 14 | 11 | 25 |
| 第二种剂量 | 6 | 19 | 25 |
| 总计 | 20 | 30 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数f′(x),的图象如图所示,
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数f′(x),的图象如图所示,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 4 | 1.5 | 4 | 1 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com