
分析 (1)设等差数列{an}的公差为d≠0,由a2,a6,a14成等比数列.可得${a}_{6}^{2}$=a2•a14,即(6+5d)2=(6+d)(6+13d),化简即可得出.
(2)bn=$\frac{2}{{(n+1){a_n}}}$=$\frac{2}{(n+1)(2n+4)}$=$\frac{1}{n+1}-\frac{1}{n+2}$,利用“裂项求和”方法即可得出.
解答 解:(1)设等差数列{an}的公差为d≠0,∵a2,a6,a14成等比数列.∴${a}_{6}^{2}$=a2•a14,
∴(6+5d)2=(6+d)(6+13d),化为d2-2d=0,d≠0,解得d=2.
所以an=6+2(n-1)=2n+4.
(2)bn=$\frac{2}{{(n+1){a_n}}}$=$\frac{2}{(n+1)(2n+4)}$=$\frac{1}{n+1}-\frac{1}{n+2}$,
∴数列{bn}的前n项和Sn═+$(\frac{1}{3}-\frac{1}{4})$+…+$(\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{1}{2}-\frac{1}{n+2}$=$\frac{n}{2(n+2)}$.
点评 本题考查了“裂项求和”方法、等差数列与等比数列的通项公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,8,0) | B. | (0,2,0) | C. | (0,8,0)或(0,2,0) | D. | (0,-8,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:| 月份 | 2 | 3 | 4 | 5 |
| 产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
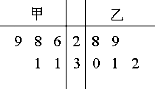 为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
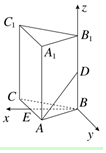 在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为$\frac{\sqrt{6}}{4}$.
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为$\frac{\sqrt{6}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com