
 利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:| 月份 | 2 | 3 | 4 | 5 |
| 产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
分析 (1)由数据表可得四个点的坐标,在坐标系中描点作图;
(2)利用最小二乘法求得回归直线方程的系数b,再求系数a,得回归直线方程;
(3)把x=6代入回归直线方程,求得预报变量y的值.
解答 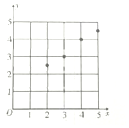 解:(1)散点图如图所示;
解:(1)散点图如图所示;
(2)$\overline{x}$=3.5,$\overline{y}$=3.5,$\sum_{i=1}^{4}{x}_{i}{y}_{i}$=52.5,$\sum_{i=1}^{4}{{x}_{i}}^{2}$=54,
∴$\stackrel{∧}{b}$=0.7,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=1.05,
∴$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+0.7x+1.05;
(3)x=6,$\stackrel{∧}{y}$=0.7×6+1.05=5.25吨.
点评 本题考查了线性回归方程的求法及应用,熟练掌握最小二乘法求回归直线方程的系数是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
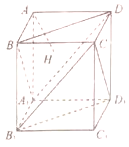 如图,在正方体ABCD-A1B1C1D1中,过点A作平面A1BD的垂线,垂足为点H,给出以下命题:①H是△A1BD的垂心;②AH垂直于平面CB1D1;③AH的延长线过点C1;④直线AH和BB1所成角的大小为45°,其中正确的命题个数为( )
如图,在正方体ABCD-A1B1C1D1中,过点A作平面A1BD的垂线,垂足为点H,给出以下命题:①H是△A1BD的垂心;②AH垂直于平面CB1D1;③AH的延长线过点C1;④直线AH和BB1所成角的大小为45°,其中正确的命题个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com