练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知各项均为正数的数列{an}的前n项和为Sn,首项为a1,且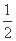,an,Sn成等差数列.

    (1)求数列{an}的通项公式;

    (2)若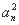=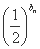,设cn=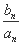,求数列{cn}的前n项和Tn.


    解:(1)由题意知2an=Sn+,an>0,

    当n=1时,2a1=a1+,∴a1=.

    当n≥2时,Sn=2an-,

    Sn-1=2an-1-,

    两式相减得an=2an-2an-1,

    整理得=2,

    ∴数列{an}是以为首项,2为公比的等比数列.

    an=a1·2n-1=×2n-1=2n-2.

    (2) ==22n-4,

    ∴bn=4-2n,

    ∴cn==,

    即cn=.

    则Tn=c1+c2+c3+…+cn,

    即Tn=+++…+.

    ∴Tn=+++…+,

    则Tn=4+++…+-.

    Tn=8-(++…+)+

    =8-+

    =8-8(1-)+

    =+

    =+=.

    即Tn=.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    上图是抛物线形拱桥，当水面在l时，拱顶离水面2米，水面宽4米，水位下降2米后，水面宽________米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn为等比数列{an}的前n项和,8a2+a5=0,则等于(　　)

    (A)-11  (B)-8   (C)5    (D)11

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn是公差不为0的等差数列{an}的前n项和,且S1,S2,S4成等比数列,则等于(　　)

    (A)1    (B)2    (C)3    (D)4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=3x+1上,n∈N*.

    (1)当实数t为何值时,数列{an}是等比数列?

    (2)在(1)的结论下,设bn=log4an+1,cn=an+bn,Tn是数列{cn}的前n项和,求Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则Sn等于(　　)

    (A)2n-1 (B)n-1  (C)n-1  (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等差数列{an}中,a7=4,a19=2a9.

    (1)求{an}的通项公式;

    (2)设bn=,求数列{bn}的前n项和Sn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给定函数①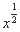y=,②y=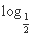 (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是(　　)

    (A)①② (B)②③

    (C)③④ (D)①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)=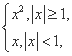g(x)是二次函数.若f[g(x)]的值域是[0,+∞),则g(x)的值域是(　　)

    (A)(-∞,-1]∪[1,+∞)    (B)(-∞,-1]∪[0,+∞)(C)[0,+∞)           (D)[1,+∞)

    查看答案和解析>>

    同步练习册答案