
���� ��1������֪�ã�a1��a3��a8�ɵȱ����У��Ӷ�4d2=3a1d���ɴ������$\frac{a_1}{d}$��ֵ��
��2��������{kn}Ϊ�ȱ����У���${k_2}^2={k_1}{k_3}$���Ƶ���$\frac{a_1}{d}=1$���Ӷ�${a_{k_n}}={k_n}d$������${k_n}={k_1}{q^{n-1}}$���ɴ˵õ���$\frac{a_1}{d}=1$ʱ������{kn}Ϊ�ȱ����У�
��3��������{kn}Ϊ�ȱ����У�a1=d��${k_n}={k_1}{q^{n-1}}��q��1��$���õ�${a_1}��\frac{{2{k_1}{q^{n-1}}}}{{n+{k_1}{q^{n-1}}}}$��$0��\frac{1}{a_1}��\frac{{n+{k_1}{q^{n-1}}}}{{2{k_1}{q^{n-1}}}}=\frac{1}{2}+\frac{q}{{2{k_1}}}\frac{n}{q^n}$���������֤�������������ʵ���ţ�0���ţ�1�����ܴ���������n1��ʹ��$\frac{n_1}{{{q^{n_1}}}}����$��
Ҫ֤$\frac{n_1}{{{q^{n_1}}}}����$����֤lnn1��n1lnq+ln�ţ��ɴ������a1��ȡֵ��Χ��
��� �⣺��1������֪�ɵã�a1��a3��a8�ɵȱ����У�
����${��{a_1}+2d��^2}={a_1}��{a_1}+7d��$����2��
�����ɵã�4d2=3a1d��
��Ϊd��0������$\frac{a_1}{d}=\frac{4}{3}$�� ��4��
��2��������{kn}Ϊ�ȱ����У���${k_2}^2={k_1}{k_3}$��
����Ϊ${a_{k_1}}$��${a_{k_2}}$��${a_{k_3}}$�ɵȱ����У�
����$[{{a_1}+��{k_1}-1��d}][{{a_1}+��{k_3}-1��d}]={[{{a_1}+��{k_2}-1��d}]^2}$��
��������${a_1}��2{k_2}-{k_1}-{k_3}��=d��{k_1}{k_3}-{k_2}^2-{k_1}-{k_3}+2{k_2}��$��
��Ϊ${k_2}^2={k_1}{k_3}$������a1��2k2-k1-k3��=d��2k2-k1-k3����
��Ϊ2k2��k1+k3������a1=d����$\frac{a_1}{d}=1$����6��
��$\frac{a_1}{d}=1$ʱ��an=a1+��n-1��d=nd������${a_{k_n}}={k_n}d$��
����Ϊ${a_{k_n}}={a_{k_1}}{q^{n-1}}={k_1}d{q^{n-1}}$������${k_n}={k_1}{q^{n-1}}$��
����$\frac{{{k_{n+1}}}}{k_n}=\frac{{{k_1}{q^n}}}{{{k_1}{q^{n-1}}}}=q$������{kn}Ϊ�ȱ����У�
���ϣ���$\frac{a_1}{d}=1$ʱ������{kn}Ϊ�ȱ����У���8��
��3����Ϊ����{kn}Ϊ�ȱ����У��ɣ�2��֪a1=d��${k_n}={k_1}{q^{n-1}}��q��1��$��
${a_{k_n}}={a_{k_1}}{q^{n-1}}={k_1}d{q^{n-1}}={k_1}{a_1}{q^{n-1}}$��an=a1+��n-1��d=na1��
��Ϊ��������n��N*������ʽ${a_n}+{a_{k_n}}��2{k_n}$�������
���Բ���ʽ$n{a_1}+{k_1}{a_1}{q^{n-1}}��2{k_1}{q^{n-1}}$��
��${a_1}��\frac{{2{k_1}{q^{n-1}}}}{{n+{k_1}{q^{n-1}}}}$��$0��\frac{1}{a_1}��\frac{{n+{k_1}{q^{n-1}}}}{{2{k_1}{q^{n-1}}}}=\frac{1}{2}+\frac{q}{{2{k_1}}}\frac{n}{q^n}$���������10��
����֤���������������ʵ���ţ�0���ţ�1�����ܴ���������n1��ʹ��$\frac{n_1}{{{q^{n_1}}}}����$��
Ҫ֤$\frac{n_1}{{{q^{n_1}}}}����$����֤lnn1��n1lnq+ln�ţ�
��Ϊ$lnx��\frac{1}{e}x��\frac{1}{2}x$����$ln{n_1}=2ln{n_1}^{\frac{1}{2}}��{n_1}^{\frac{1}{2}}$��
�ⲻ��ʽ${n_1}^{\frac{1}{2}}��{n_1}lnq+ln��$����${��{n_1}^{\frac{1}{2}}��^2}lnq-{n_1}^{\frac{1}{2}}+ln�ţ�0$��
�ɵ�${n_1}^{\frac{1}{2}}��\frac{{1+\sqrt{1-4lnqln��}}}{2lnq}$������${n_1}��{��\frac{{1+\sqrt{1-4lnqln��}}}{2lnq}��^2}$��
����ȡ${n_0}=[{{{��\frac{{1+\sqrt{1-4lnqln��}}}{2lnq}��}^2}}]+1$����n1��n0ʱ��ԭʽ��֤��
����$0��\frac{1}{a_1}��\frac{1}{2}$������a1��2������a1��ȡֵ��Χ��[2��+�ޣ��� ��16��
���� ���⿼��Ȳ����е������빫��ı�ֵ������������ȱ����еĵȲ����е������빫��ı�ֵ��ȷ�����������е������ȡֵ��Χ�����ۺ���ǿ���Ѷȴ���ѧ˼άҪ��ϸߣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1} | B�� | {2} | C�� | {3} | D�� | {2��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
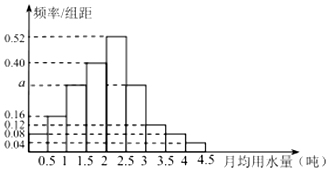 �ҹ�������������ȱˮ�Ĺ��ң�����ȱˮ�����Ϊͻ����ij������Ϊ�˹��������Լ��ˮ���ƻ��ڱ������о���������ˮ�����������ȷ��һ�������ľ�������ˮ����x���֣�����ˮ��������x�IJ��ְ�ƽ���շѣ�����x�IJ��ְ�����շѣ�Ϊ���˽�ȫ��������ˮ���ķֲ������ͨ�������������100λ����ij�������ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1��������[4��4.5]�ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
�ҹ�������������ȱˮ�Ĺ��ң�����ȱˮ�����Ϊͻ����ij������Ϊ�˹��������Լ��ˮ���ƻ��ڱ������о���������ˮ�����������ȷ��һ�������ľ�������ˮ����x���֣�����ˮ��������x�IJ��ְ�ƽ���շѣ�����x�IJ��ְ�����շѣ�Ϊ���˽�ȫ��������ˮ���ķֲ������ͨ�������������100λ����ij�������ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1��������[4��4.5]�ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��2.25�� | B�� | ��2.25��2.5�� | C�� | ��2.5��2.75�� | D�� | ��2.75��3�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com