
 如图为一简单几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=DA=2,EC=1,N为线段PB的中点.
如图为一简单几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=DA=2,EC=1,N为线段PB的中点.分析 (Ⅰ)连结AC与BD交于点F,则F为BD的中点,连结NF,推导出四边形NFCE为平行四边形,从而NE∥AC,推导出AC⊥PD,由此能证明NE⊥PD.
(Ⅱ)推导出平面PDCE⊥平面ABCD,从而BC是四棱锥B-PDCE的高,由此能法语出四棱锥B-CEPD的体积.
解答 证明:(Ⅰ)连结AC与BD交于点F,则F为BD的中点,连结NF,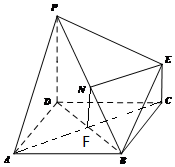
∵N为线段PB的中点,∴NF∥PD,且NF=$\frac{1}{2}$PD,…(3分)
又EC∥PD,且EC=$\frac{1}{2}PD$,
∴NF∥EC,且NF=EC,∴四边形NFCE为平行四边形,(5分)
∴NE∥FC,即NE∥AC. (6分)
又∵PD⊥平面ABCD,AC?面ABCD,∴AC⊥PD,
∵NE∥AC,∴NE⊥PD.(7分)
解:(Ⅱ)∵PD⊥平面ABCD,PD?平面PDCE,
∴平面PDCE⊥平面ABCD.(9分)
∵BC⊥CD,平面PDCCE∩平面ABCD=CD,BC?平面ABCD,
∴BC⊥平面PDCE.(10分)
∴BC是四棱锥B-PDCE的高.(11分)
∵${S}_{梯形PDCE}=\frac{1}{2}(PD+EC)•DC$=$\frac{1}{2}×3×2=3$,(12分)
∴四棱锥B-CEPD的体积VB-CEPD=$\frac{1}{3}{S}_{梯形PDCE}•BC$=$\frac{1}{3}×3×2=2$.
点评 本题考查线线垂直的证明,考查几何体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | |a|≥1且|b|≥1 | B. | |a|≤1且|b|≤1 | C. | (|a|-1)(|b|-1)≥0 | D. | (|a|-1)(|b|-1)≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第二象限的角比第一象限的角大 | |
| B. | 角α是第四象限角的充要条件是2kπ-$\frac{π}{2}$<α<2kπ(k∈Z) | |
| C. | 第一象限的角是锐角 | |
| D. | 三角形的内角是第一象限角或第二象限角? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≤1 | B. | 1≤k≤2 | C. | k≥1 | D. | k≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com