Question

11．若关于x的方程$\sqrt{3}$sinx+|cosx|+a=0在区间[0，2π]内有四个不同的解分别为x₁，x₂，x₃，x₄，则x₁+x₂+x₃+x₄的值为2π．

Answer 1

分析 分类讨论，化简f（x）=$\sqrt{3}$sinx+|cosx|的解析式，由题意可得，f（x）的图象和直线y=-a在区间[0，2π]内有四个不同的交点，再利用正弦函数的图象的对称性，求得x₁+x₂+x₃+x₄的值．

解答 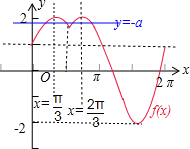解：由题意可得函数f（x）=$\sqrt{3}$sinx+|cosx|=$\left\{\begin{array}{l}{2sin（x+\frac{π}{6}），x∈[0，\frac{π}{2}]}\\{2sin（x-\frac{π}{6}），x∈（\frac{π}{2}，\frac{3π}{2}]}\\{2sin（x+\frac{π}{6}），x∈（\frac{3π}{2}，2π]}\end{array}\right.$ 的图象
和直线y=-a在区间[0，2π]内有四个不同的交点，1＜-a＜2，即-2＜a＜-1．
故x₁+x₂ =2×$\frac{π}{3}$=$\frac{2π}{3}$，x₃+x₄ =2×$\frac{2π}{3}$=$\frac{4π}{3}$，
∴x₁+x₂+x₃+x₄=$\frac{2π}{3}$+$\frac{4π}{3}$2π，
故答案为：2π．

点评 本题主要考查两角和差的正弦公式，函数的零点和方程根的关系，正弦函数的图象的对称性，体现了转化、分类讨论的数学思想，属于中档题．