考点:简单线性规划
专题:不等式的解法及应用
分析:先标出已知不等式组表示的平面区域,根据围成此区域的多边形特征探求其面积.
解答:
解:如右图所示,在同一坐标系中分别作出直线l
1:x+y=4,l
2:x-y=2
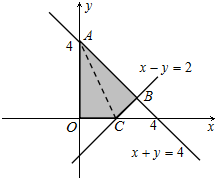
于是得到不等式组
表示的平面区域,即四边形OABC(含边界),
连结AC,则S
四边形0ABC=S
Rt△OAC+S
△ABC,
由A(0,4),C(2,0)知,直线AC的方程为2x+y-4=0,且|AC|=
2,
由
得B(3,1),从而点B到直线AC的距离d=
=,
所以S
△ABC=
|AC|•d=
×2×=3,
又S
Rt△OAC=
|OC|•|OA|=
×2×4=4,
所以S
四边形OABC=4+3=7,即原不等式组表示的平面区域的面积为7.
故答案为:7.
点评:1.本题主要考查了不等式组表示的平面区域的应用,平面内的距离公式等,考查了数形结合思想、化归思想,解决本题的关键有两个:一是正确作出不等式组表示的平面区域,二是善于将面积进行转化.
2.对于面积的求解,首先应弄清区域的形状,若为三角形,一般根据“
S=×底×高”求解,底可以由两点间距离公式得到,高可以由点到直线的距离公式得到;若为四边形或四边以上的多边形,一般将其拆分为几个易求的三角形或四边形求解.




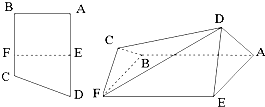 如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起成如图的位置,使AD=AE.
如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起成如图的位置,使AD=AE.