
分析 通过平方以及二倍角公式化简求解即可.
解答 解:cosα=$\frac{12}{13}$,α∈($\frac{3π}{2}$,2π),
可得sinα=$-\sqrt{1-co{s}^{2}α}$=-$\frac{5}{13}$.
则(sin$\frac{α}{2}$-cos$\frac{α}{2}$)2=cos2$\frac{α}{2}$-2sin$\frac{α}{2}$cos$\frac{α}{2}$+cos2$\frac{α}{2}$=1-sinα=1+$\frac{5}{13}$=$\frac{18}{13}$.
点评 本题考查三角函数的化简求值,二倍角公式的应用,考查计算能力.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
 如图,矩形ORTM内放置6个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则$(\overrightarrow{AE}-\overrightarrow{BC})•\overrightarrow{BD}$=-6.
如图,矩形ORTM内放置6个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则$(\overrightarrow{AE}-\overrightarrow{BC})•\overrightarrow{BD}$=-6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第6项 | B. | 第7项 | C. | 第11项 | D. | 第6项和第7项 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
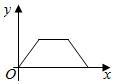 如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )
如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )| A. |  | B. |  | C. | 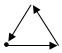 | D. | 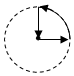 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com