考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由
f′(x)=x-a+==,得当a-1>1时,即a>2时,f(x)的单调增区间为(0,1),(a-1,+∞);单调减区间为(1,a-1).当a-1=1时,即a=2时,f(x)的单调增区间为(0,+∞)
(Ⅱ)要证:对任意
x1,x2∈(0,+∞),≠x2,有
>-1.即证f(x
1)+x
1>f(x
2)+x
2设
g(x)=f(x)+x=x2-(a-1)x+(a-1)lnx,x>0,即证g(x)在(0,+∞)单调递增.由
g′(x)=x-(a-1)+=,由g(x)在(0,+∞)单调递增,从而原题得证.
解答:
解:(Ⅰ)f(x)的定义域为(0,+∞),
f′(x)=x-a+==,
∵a-1≥1
当a-1>1时,即a>2时,f(x)的单调增区间为(0,1),(a-1,+∞);
单调减区间为(1,a-1).
当a-1=1时,即a=2时,f(x)的单调增区间为(0,+∞)
(Ⅱ)要证:对任意
x1,x2∈(0,+∞),≠x2,
有
>-1.
不防设x
1>x
2,
即证f(x
1)-f(x
2)>-(x
1-x
2)
即证f(x
1)+x
1>f(x
2)+x
2设
g(x)=f(x)+x=x2-(a-1)x+(a-1)lnx,x>0
即证当x
1>x
2时,g(x
1)>g(x
2).
即证g(x)在(0,+∞)单调递增.
∵
g′(x)=x-(a-1)+=而△=(a-1)
2-4(a-1)=(a-1)(a-5)
又∵2≤a<5,
∴△<0,
∴x
2-(a-1)x+(a-1)>0恒成立,
∴
g′(x)=>0对x∈(0,+∞)恒成立,
∴g(x)在(0,+∞)单调递增.
∴原题得证.
点评:本题考察了函数的单调性,导数的应用,不等式的证明,是一道综合题.



 阅读快车系列答案
阅读快车系列答案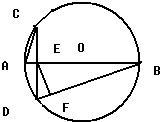 如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F.
如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F.