
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)解关于导函数的不等式,求出a的范围即可.
解答 解:(Ⅰ)f(x)的 定义域为(-∞,$\frac{1}{2}$],
导函数f′(x)=$\frac{-x(5x+3a-2)}{\sqrt{1-2x}}$,
当a=$\frac{17}{3}$,f′(x)=$\frac{-5x(x+3)}{\sqrt{1-2x}}$,
| x | (-∞,-5) | -5 | (-5,0) | 0 | (0,$\frac{1}{2}$) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | 递减 | 极小值 | 递增 | 极大值 | 递减 |
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
 如图,AB是圆O的直径,P是圆弧$\widehat{AB}$上的点,M,N是直径AB上关于O对称的两点,且AB=4,MN=2,则$\overrightarrow{PM}$•$\overrightarrow{PN}$等于( )
如图,AB是圆O的直径,P是圆弧$\widehat{AB}$上的点,M,N是直径AB上关于O对称的两点,且AB=4,MN=2,则$\overrightarrow{PM}$•$\overrightarrow{PN}$等于( )| A. | 3 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 随t的变化而变化 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “∥”后面是注释内容,对程序运行起着重要作用 | |
| B. | “∥”后面是程序执行的指令,对程序运行起着重要作用 | |
| C. | “∥”后面是注释内容,对程序运行不起作用 | |
| D. | “∥”后面是程序执行的指令,对程序运行不起作用 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α∥β,l?α,n?β,则l∥n | B. | 若α⊥β,l?α,则l⊥β | ||
| C. | 若l⊥α,l∥β,则α⊥β | D. | 若l⊥n,m⊥n,则l∥m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{9}{16}$ | C. | $\frac{9}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
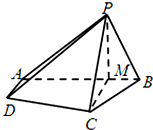 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com